
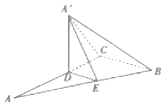
【题目】如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
科目:高中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数,例如:[π]=3. S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3
]=3
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10
]=10
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+
]+ ![]() ]=21,
]=21,
…,
依此规律,那么S10=( )
A.210
B.230
C.220
D.240
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数),其图像是曲线
为常数),其图像是曲线![]() .
.
(1)设函数![]() 的导函数为
的导函数为![]() ,若存在三个实数
,若存在三个实数![]() ,使得
,使得![]() 与
与![]() 同时成立,求实数
同时成立,求实数![]() 的取值范围;
的取值范围;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,在点
上的动点,在点![]() 处作曲线
处作曲线![]() 的切线
的切线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,在点
,在点![]() 处作曲线
处作曲线![]() 的切线
的切线![]() ,设切线
,设切线![]() 的斜率分别为
的斜率分别为![]() ,问:是否存在常数
,问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )单调,则ω的最大值为 .
)单调,则ω的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
(Ⅰ)写出m,n的值,若该“微信运动”团队共有120人,请估计该团队中一天行走步数不少于7500步的人数;
(Ⅱ)记C组步数数据的平均数与方差分别为v1, ![]() ,E组步数数据的平均数与方差分别为v2,
,E组步数数据的平均数与方差分别为v2, ![]() ,试分别比较v1与v2,
,试分别比较v1与v2, ![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1 , AB,BB1 , B1C1的中点,则异面直线EF与GH所成的角等于( ) 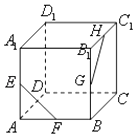
A.45°
B.60°
C.90°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com