
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )单调,则ω的最大值为 .
)单调,则ω的最大值为 .
【答案】9
【解析】解:∵函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴, ∴ω(﹣
为y=f(x)图象的对称轴, ∴ω(﹣ ![]() )+φ=nπ,n∈Z,且ω
)+φ=nπ,n∈Z,且ω ![]() +φ=n′π+
+φ=n′π+ ![]() ,n′∈Z,
,n′∈Z,
∴相减可得ω ![]() =(n′﹣n)π+
=(n′﹣n)π+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,即ω=2k+1,即ω为奇数.
,k∈Z,即ω=2k+1,即ω为奇数.
∵f(x)在( ![]() ,
, ![]() )单调,
)单调,
(Ⅰ)若f(x)在( ![]() ,
, ![]() )单调递增,
)单调递增,
则ω ![]() +φ≥2kπ﹣
+φ≥2kπ﹣ ![]() ,且ω
,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z,
,k∈Z,
即﹣ω ![]() ﹣φ≤﹣2kπ+
﹣φ≤﹣2kπ+ ![]() ①,且ω
①,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z ②,
,k∈Z ②,
把①②可得 ![]() ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
当ω=11时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .
.
此时f(x)=sin(11x﹣ ![]() )在(
)在( ![]() ,
, ![]() )上不单调,不满足题意.
)上不单调,不满足题意.
当ω=9时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=
,∴φ= ![]() ,
,
此时f(x)=sin(9x+ ![]() )在(
)在( ![]() ,
, ![]() )上单调递减,不满足题意;
)上单调递减,不满足题意;
故此时ω无解.
(Ⅱ)若f(x)在( ![]() ,
, ![]() )单调递减,
)单调递减,
则ω ![]() +φ≥2kπ+
+φ≥2kπ+ ![]() ,且ω
,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z,
,k∈Z,
即﹣ω ![]() ﹣φ≤﹣2kπ﹣
﹣φ≤﹣2kπ﹣ ![]() ③,且ω
③,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z ④,
,k∈Z ④,
把③④可得 ![]() ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
当ω=11时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .
.
此时f(x)=sin(11x﹣ ![]() )在(
)在( ![]() ,
, ![]() )上不单调,不满足题意.
)上不单调,不满足题意.
当ω=9时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=
,∴φ= ![]() ,
,
此时f(x)=sin(9x+ ![]() )在(
)在( ![]() ,
, ![]() )上单调递减,满足题意;
)上单调递减,满足题意;
故ω的最大值为9.
故答案为:9.
先跟据正弦函数的零点以及它的图象的对称性,判断ω为奇数,由f(x)在( ![]() ,
, ![]() )单调,分f(x)在(
)单调,分f(x)在( ![]() ,
, ![]() )单调递增、单调递减两种情况,分别求得ω的最大值,综合可得它的最大值.
)单调递增、单调递减两种情况,分别求得ω的最大值,综合可得它的最大值.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】先后掷子(子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x+y为偶数”,事件B为“x,y中有偶数且x≠y”,则概率P(B|A)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,
中, ![]() :
: ![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程,并说明它们分别表示什么曲线;
的直角坐标方程,并说明它们分别表示什么曲线;
(2)若![]() 分别为
分别为![]() ,
, ![]() 上的动点,且
上的动点,且![]() 的最小值为2,求
的最小值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
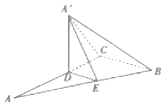
【题目】如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=log2an,Tn为{bn}的前n项和,求证![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.
(1)求A中学至少有1名学生入选代表队的概率;
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z在复平面内对应的点在第四象限,且z是方程x2﹣4x+5=0的根.
(1)求复数z;
(2)复数w=a﹣ ![]() (a∈R)满足|w﹣z|<2
(a∈R)满足|w﹣z|<2 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com