
【题目】如图,在底面边长为![]() 、高为
、高为![]() 的正六棱柱
的正六棱柱![]() 展厅内,长为
展厅内,长为![]() ,宽为
,宽为![]() 的矩形油画
的矩形油画![]() 挂在厅内正前方中间.
挂在厅内正前方中间.
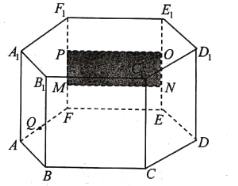
(1)求证:平面![]() 平面
平面![]() ;
;
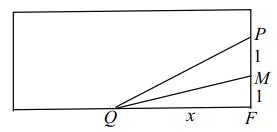
(2)当游客![]() 在
在![]() 上看油画的纵向视角(即
上看油画的纵向视角(即![]() )最大时,求
)最大时,求![]() 与油画平面所成的角.
与油画平面所成的角.
【答案】(1)证明见解析(2)![]() .
.
【解析】
(1)连结![]() ,
,![]() ,可证
,可证![]() ,
,![]() ,即可得到
,即可得到![]() 面
面![]() ,从而得证;
,从而得证;
(2)在矩形![]() 中,设
中,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,利用两角差的正切公式表示出
,利用两角差的正切公式表示出![]() ,再利用基本不等式求出
,再利用基本不等式求出![]() 的最值,过
的最值,过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() 点,连结
点,连结![]() ,
,![]() ,则
,则![]() 就是
就是![]() 与面
与面![]() 所成的角,再由勾股定理计算可得;
所成的角,再由勾股定理计算可得;
解:(1)连结![]() ,
,![]() ,因在正六棱柱
,因在正六棱柱![]() 中,
中,
底面![]() 是正六边形,
是正六边形,![]() ,
,
又![]() ,所以
,所以![]() ,
,
则![]() ,
,![]() ,
,
因![]() 是矩形,所以
是矩形,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,又
,又![]() 面
面![]() ,
,
所以平面![]() 平面
平面![]() .
.
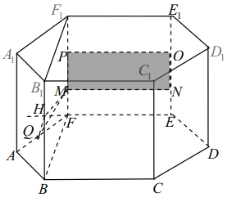
(2)在矩形![]() 中,设
中,设![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
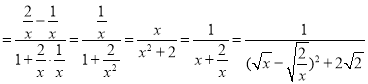 ,
,
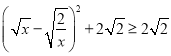 ,当
,当![]() 时等号成立.
时等号成立.
所以![]() ,故当
,故当![]() 时,即
时,即![]() ,
,![]() 最大.
最大.
过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() 点,连结
点,连结![]() ,
,![]() .
.
在正六棱柱![]() 中,
中,
![]() 面
面![]() ,
,![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,
,
面![]() 面
面![]() ,
,![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,则
,则![]() 为
为![]() 在面
在面![]() 内的射影,
内的射影,
故![]() 就是
就是![]() 与面
与面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
故游客![]() 在
在![]() 上看油画的纵向视角最大时,
上看油画的纵向视角最大时,![]() 与油画平面所成的角为
与油画平面所成的角为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次商品的有奖销售活动中,有![]() 人获三等奖.三等奖的奖品共有四种,每个三等奖获得者随意从四种奖品中挑选一种,结果有一种奖品无人挑选的概率是______.
人获三等奖.三等奖的奖品共有四种,每个三等奖获得者随意从四种奖品中挑选一种,结果有一种奖品无人挑选的概率是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值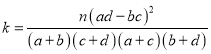
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中在校学生2000人![]() 为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动
为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动![]() 每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
高一年级 | 高二年级 | 高三年级 | |
跑步 | a | b | c |
登山 | x | y | z |
其中a:b:![]() :3:5,全校参与登山的人数占总人数的
:3:5,全校参与登山的人数占总人数的![]() ,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取
,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取![]()
![]()
A. 6人B. 12人C. 18人D. 24人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0、1、2、3、4这五个数字组成无重复数字的五位数,其中恰有一个偶数数字夹在两个奇数数字之间的五位数的个数是( )
A.48 B.36 C.28 D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,a1=3,且Sn=nan+1-n2-n.
(1)求{an}的通项公式;
(2)若数列{bn}满足![]() ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com