
【题目】已知正项数列![]() 为等比数列,等差数列
为等比数列,等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:
![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)设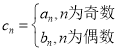 ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用等差数列的有关知识建立方程组求解;(2)借助题设运用错位相减法求和;(3)依据题设运用分类整合思想分析推证和探求.
试题解析:
(1)因为数列![]() 为等差数列,且
为等差数列,且![]() ,
,
即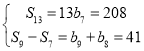 ,解得
,解得![]() ,公差为3,.............2分
,公差为3,.............2分
所以![]() ,得
,得![]() ..............3分
..............3分
又![]() ,
,
所以![]() ....................5分
....................5分
(2)![]() ,.........①
,.........①
则![]() ,..............②
,..............②
将①—②得:
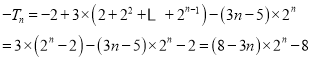
所以![]() ...................8分
...................8分
(3)因为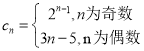 ,
,
当![]() 时,
时,![]() ,不等,...........9分
,不等,...........9分
当![]() 时,
时,![]() ,
,
![]() 成立,...............10分
成立,...............10分
当![]() 且为奇数时,
且为奇数时,![]() 为偶数,
为偶数,![]() 为奇数,
为奇数,
所以![]() 为偶数,
为偶数,![]() 为奇数,不成立,.............12分
为奇数,不成立,.............12分
当![]() ,且
,且![]() 为偶数时,若
为偶数时,若![]() ,
,
即![]() ,..................13分
,..................13分
得![]() .............(*)
.............(*)
因为![]() ,所以(*)不成立.......15分
,所以(*)不成立.......15分
综上得![]() ............................16分
............................16分


科目:高中数学 来源: 题型:
【题目】如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线![]() 对称,又圆
对称,又圆![]() 与直线
与直线![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() .
.
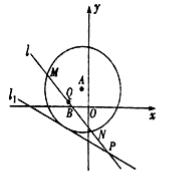
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)![]() 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量依次为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量![]() (单位:万件)与月份
(单位:万件)与月份![]() 的关系. 模拟函数
的关系. 模拟函数![]() ;模拟函数
;模拟函数![]() .
.
(1)已知4月份的产量为万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过点
,过点![]() ,
,![]() 的直线与原点的距离为
的直线与原点的距离为![]() ,
,![]() 是椭圆上任一点,从原点
是椭圆上任一点,从原点![]() 向圆
向圆![]() :
:![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() ,
,![]() .
.
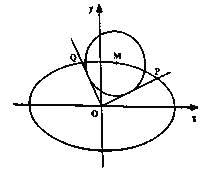
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在五棱锥![]() 中,
中,![]() ,且
,且![]() .
.
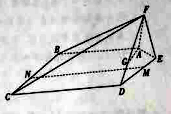
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求直线
恰好重合,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
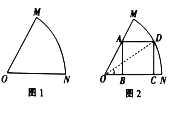
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com