
����Ŀ��ij��λ��Ҫ�Ӽס���![]() ����ѡ��һ�˲μ��¸�λ��ѵ���ر���֯��
����ѡ��һ�˲μ��¸�λ��ѵ���ر���֯��![]() ��ר��Ŀ��ԣ��ɼ�ͳ�����£�
��ר��Ŀ��ԣ��ɼ�ͳ�����£�
��һ�� | �ڶ��� | ������ | ������ | ������ | |
�ijɼ� |
|
|
|
|
|
�ҵijɼ� |
|
|
|
|
|
��1�������й�ͳ��֪ʶ���ش�����:���Ӽס���![]() ����ѡ��
����ѡ��![]() �˲μ��¸���ѵ������Ϊѡ˭���ʣ���˵�����ɣ�
�˲μ��¸���ѵ������Ϊѡ˭���ʣ���˵�����ɣ�
��2�������йؘ���֪ʶ������������⣺
�Ӽס���![]() �˵ijɼ��и������ȡһ������鵽�ijɼ�Ϊ
�˵ijɼ��и������ȡһ������鵽�ijɼ�Ϊ![]() ���鵽�ҵijɼ�Ϊ
���鵽�ҵijɼ�Ϊ![]() ����
����![]() ��ʾ��������
��ʾ��������![]() ���¼������¼�
���¼������¼�![]() �ĸ���.
�ĸ���.
���𰸡�(1) �ɼ��ʺϣ�(2) ![]()
�������������������1���������߳ɼ���ƽ�����ͷ��ƽ������ȣ���ѡ���С�ıȽ��ȶ�.��2�������оٷ��г����еĿ�������![]() �֣����з����������
�֣����з����������![]() �֣��ɴ���ø���Ϊ
�֣��ɴ���ø���Ϊ![]() .
.
���������
(1)��ƽ���ɼ�Ϊ![]() ���ҵ�ƽ���ɼ�Ϊ
���ҵ�ƽ���ɼ�Ϊ![]() ���ʼ��Ҷ��˵�ƽ��ˮƽһ��. �ijɼ�����
���ʼ��Ҷ��˵�ƽ��ˮƽһ��. �ijɼ�����![]() ���ҵijɼ�����
���ҵijɼ�����![]() ��
�� ![]() ����Ӧ�ɼ��ʺ�.
����Ӧ�ɼ��ʺ�.
(2)�Ӽ��Ҷ��˵ijɼ��и������һ������׳鵽�ijɼ�Ϊ![]() ���ҳ鵽�ijɼ�Ϊ
���ҳ鵽�ijɼ�Ϊ![]() �������е�
�������е�![]() ��
��![]()
![]()
![]()
![]()
![]() ��
��![]() ����������������
����������������![]() ����
���� ![]() ����
����![]() ���������¼��ĸ���Ϊ
���������¼��ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ����
����![]() ��
�� ![]() .
.
��1��֤��������![]() �ǵȲ����У�
�ǵȲ����У�
��2����![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ���������
���������![]() ��
�� ![]() ��
�� ![]() �������������
�������������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĵ���Ϊֱ�����Σ�
�ĵ���Ϊֱ�����Σ�![]()
![]() ��ƽ��
��ƽ��![]() ����
����![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ�������Σ�
��������![]() ����
����![]() �ϵ�һ��(���ڶ˵�).
�ϵ�һ��(���ڶ˵�).
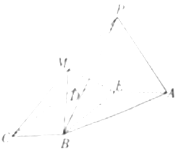
��������![]() Ϊ
Ϊ![]() �е㣬��֤��
�е㣬��֤��![]() ƽ��
ƽ��![]() ��
��
�������Ƿ���ڵ�![]() ��ʹ�����
��ʹ�����![]() �Ĵ�СΪ30��.�����ڣ������
�Ĵ�СΪ30��.�����ڣ������![]() ��λ�ã��������ڣ�˵������.
��λ�ã��������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ��ǧԪ����������
����λ��ǧԪ����������![]() ����λ����Ԫ����Ӱ�죬�Խ�5���������
����λ����Ԫ����Ӱ�죬�Խ�5���������![]() ��������
��������![]() ��
��![]() ��������ͳ�ƣ��г����±���
��������ͳ�ƣ��г����±���
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
Ա��С����С��ֱ��ṩ�˲�ͬ�ķ�����
��1��С���������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ�������������
�Ĺ�ϵ�������������![]() ����
����![]() �����Իع鷽������ϵ����ȷ��0.01��
�����Իع鷽������ϵ����ȷ��0.01��
��2��С�����ѡ������ع�ģ�����![]() ��
��![]() �Ĺ�ϵ���õ��˻ع鷽����
�Ĺ�ϵ���õ��˻ع鷽����![]() �����ṩ�����ָ��
�����ṩ�����ָ��![]() ���������ָ��˵��ѡ���ĸ�ģ�����ʣ���Ԥ����������Ϊ4��Ԫ����������ȷ��0.01����С��Ҳ�ṩ�����ķ�����������
���������ָ��˵��ѡ���ĸ�ģ�����ʣ���Ԥ����������Ϊ4��Ԫ����������ȷ��0.01����С��Ҳ�ṩ�����ķ�����������![]() ��
��
�ο���ʽ�����ָ��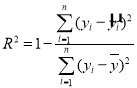
�ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
 ��
��![]() ���������
���������![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊѡ�βμӡ�ȫ�и�����ѧ��������ѡ�֣�ij��ѧ������һ�Ρ���ѧ�������.Ϊ���˽Ȿ�ξ���ѧ���ijɼ���������г�ȡ�˲���ѧ���ķ������÷�ȡ������������Ϊ![]() �֣���Ϊ��������������Ϊ
�֣���Ϊ��������������Ϊ![]() ������ͳ��.����
������ͳ��.����![]() �ķ�������Ƶ�ʷֲ�ֱ��ͼ�����������������ľ�Ҷͼ��ͼ�н��г��˵÷���
�ķ�������Ƶ�ʷֲ�ֱ��ͼ�����������������ľ�Ҷͼ��ͼ�н��г��˵÷���![]() �����ݣ�.
�����ݣ�.
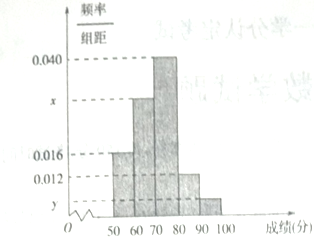
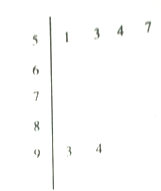
��1����������![]() ��Ƶ�ʷֲ�ֱ��ͼ��
��Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ�������ȡѧ����ƽ���֣�
��ֵ�������ȡѧ����ƽ���֣�
��2����ѡȡ�������У��Ӿ����ɼ���![]() �����ϣ���
�����ϣ���![]() ��)��ѧ���������ȡ
��)��ѧ���������ȡ![]() ��ѧ���μӡ�ȫ������ѧ������������ȡ��
��ѧ���μӡ�ȫ������ѧ������������ȡ��![]() ��ѧ����������һ�˵÷���
��ѧ����������һ�˵÷���![]() �ڵĸ���.
�ڵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��������a=��2ʱ������f(x)�ĵ������䣻
��������g(x)= ![]() +
+![]() ��
��![]() 1��+��)���ǵ�����������ʵ��a��ȡֵ��Χ.
1��+��)���ǵ�����������ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������PABCD��������ABCD��������������PD��ֱ�ڵ���ABCD��PD��DC����E��PC���е���
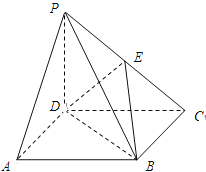
������֤��PA��ƽ��EBD��
������������EBDP������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2������![]() �ĵ������䣻
�ĵ������䣻
��3��������![]() ��ʹ��
��ʹ��![]() ��
��![]() ����Ȼ�����ĵ���������ʵ��
����Ȼ�����ĵ���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-5������ʽѡ��
��֪����![]() .
.
��I����֤��![]() �������
�������
��II��������ʵ��![]() ��ʹ��
��ʹ��![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com