【题目】数列
满足
， 
.
（1）证明：数列
是等差数列；
（2）设
，数列
的前
项和为
，对任意的
， 
， 
恒成立，求正数
的取值范围.
【答案】（1）证明见解析 （2）
【解析】试题分析：（1）根据等差数列的定义即可证明：数列
是等差数列；
（2）利用错位相减法即可求数列{bn}的前n项和
，利用作差法可得数列{
}单调递增， 
， 
恒成立，只需
即可.
试题解析：
解（1）证明：由已知可得
＝
，
即
＝
＋1，即－＝1.
∴数列
是公差为1的等差数列．
（2）由(1)知＝
＋(n－1)×1＝n＋1，
∴an＝
.
所以bn＝
，
Tn＝
＋
＋
＋…＋，
Tn＝
＋
＋
＋…＋
.
两式相减得
Tn＝＋2
－，
Tn＝＋2×
－，
Tn＝1＋4
－＝3－
，
由Tn－Tn－1＝3－－
＝，
当n≥2时，Tn－Tn－1>0，所以数列{Tn}单调递增．
最小为
，
依题意
上恒成立，
设
则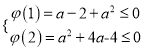
又
解得
灵星计算小达人系列答案
孟建平错题本系列答案科目：高中数学 来源： 题型：
【题目】定义在
上的单调递减函数
，对任意
都有
， 
．
（Ⅰ）判断函数
的奇偶性，并证明之；
（Ⅱ）若对任意
，不等式
（
为常实数）都成立，求
的取值范围；（Ⅲ）设
， 
， 
， 
， 
．
若
， 
，比较
的大小并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若
，求
的值；
（2）若存在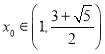
，使函数
的图像在点
和点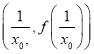
处的切线互相垂直，求
的取值范围；
（3）若函数
在区间
上有两个极值点，则是否存在实数
，使
对任意的
恒成立？若存在，求出
的取值范围，若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
（
、
为常数）．
（Ⅰ）求函数
在点
处的切线方程；
（Ⅱ）当函数
在
处取得极值
，求函数
的解析式；
（Ⅲ）当
时，设
，若函数
在定义域上存在单调减区间，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为抛物线
： 
（
）的焦点，直线
： 
交抛物线
于
， 
两点．
（Ⅰ）当
， 
时，求抛物线
的方程；
（Ⅱ）过点
， 
作抛物线
的切线， 
， 
交点为
，若直线
与直线
斜率之和为
，求直线
的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，我海监船在
岛海域例行维权巡航，某时刻航行至
处，此时测得其东北方向与它相距32海里的
处有一外国船只，且
岛位于海监船正东
海里处．
（1）求此时该外国船只与岛的距离；
（2）观测中发现，此外国船只正以每小时8海里的速度沿正南方向航行，为了将该船拦截在离岛24海里处，不让其进入岛24海里内的海域，试确定海监船的航向，并求其速度的最小值．（参考数据：
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位需要从甲、乙
人中选拔一人参加新岗位培训，特别组织了
个专项的考试，成绩统计如下：
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
（1）根据有关统计知识，回答问题:若从甲、乙
人中选出
人参加新岗培训，你认为选谁合适，请说明理由；
（2）根据有关槪率知识，解答以下问题：
从甲、乙
人的成绩中各随机抽取一个，设抽到甲的成绩为
，抽到乙的成绩为
，用
表示满足条件
的事件，求事件
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
