
(本大题12分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线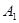 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .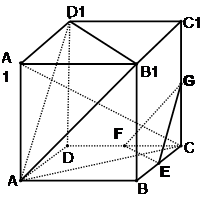
(1)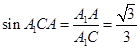 ; (2)见解析;(3)见解析。
; (2)见解析;(3)见解析。
解析试题分析:(1)因为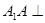 平面ABCD,所以
平面ABCD,所以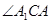 为
为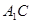 与平面ABCD所成角,
与平面ABCD所成角,
然后解三角形求出此角即可.
(2)证明面面平行根据判定定理只须证明平面平面A B1D1内两条相交直线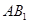 和
和 分别平行于平面EFG即可.在证明线面平行时又转化为证明线线平行.
分别平行于平面EFG即可.在证明线面平行时又转化为证明线线平行.
(3)易证:BD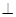 平面AA1C,再证明EF//BD,因而可证出平面AA1C⊥面EFG.
平面AA1C,再证明EF//BD,因而可证出平面AA1C⊥面EFG.
(1)∵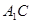
 平面ABCD=C,在正方体ABCD-A1B1C1D1
平面ABCD=C,在正方体ABCD-A1B1C1D1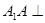 平面ABCD
平面ABCD
∴AC为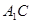 在平面ABCD的射影
在平面ABCD的射影
∴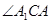 为
为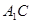 与平面ABCD所成角……….2分
与平面ABCD所成角……….2分
正方体的棱长为
∴AC=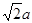 ,
,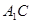 =
=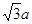
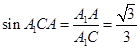 ………..4分
………..4分
(2)在正方体ABCD-A1B1C1D1
连接BD,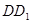 ∥
∥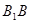 ,
,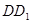 =
=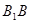
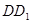
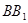 为平行四边形
为平行四边形
∴ ∥
∥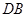 ∵E,F分别为BC,CD的中点
∵E,F分别为BC,CD的中点
∴EF∥BD∴EF∥ …………3分
…………3分
∵EF 平面GEF,
平面GEF,
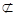 平面GEF
平面GEF
∴ ∥平面GEF …………7分
∥平面GEF …………7分
同理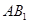 ∥平面GEF∵
∥平面GEF∵
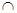
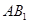 =
=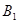
∴平面A B1D1∥平面EFG ……………9分
(3)在正方体ABCD-A1B1C1D1∴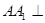 平面ABCD
平面ABCD
∵EF 平面ABCD
平面ABCD
∴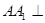 EF …………10分
EF …………10分
∵ABCD为正方形
∴AC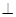 BD
BD
∵EF∥BD
∴AC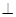 EF ………..11分
EF ………..11分
∴EF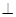 平面AA1C
平面AA1C
∵EF 平面EFG
平面EFG
∴平面AA1C⊥面EFG …………….12分.
考点:斜线与平面所成的角,线面垂直,面面垂直,面面平行的判定.
点评:斜线与平面所成的角就是斜线与它在这个平面内的射影所成的角,因而关键是找到它在这个平面内的射影.面面垂直(平行)证明要转化为证明线面垂直(平行)再转化为线线垂直(平行).


科目:高中数学 来源: 题型:解答题
已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,AB=2CD=2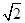 ,E,F分别是AB,AP的中点.
,E,F分别是AB,AP的中点.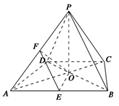
(1)求证:AC⊥EF;
(2)求二面角F-OE-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.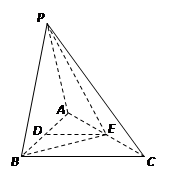
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求证:AB⊥PE;
(Ⅲ)求二面角A-PB-E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△ ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.
(Ⅰ)求证: 平面ABD;
平面ABD;
(Ⅱ)求直线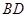 与平面
与平面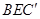 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱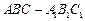 中,
中, ,顶点
,顶点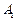 在底面
在底面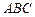 上的射影恰为点
上的射影恰为点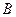 ,且
,且 .
.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)求棱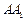 与
与 所成的角的大小;
所成的角的大小;
(Ⅲ)若点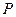 为
为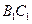 的中点,并求出二面角
的中点,并求出二面角 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
四、附加题:本大题共2小题,每小题10分,共20分。
(20)(本小题满分10分)
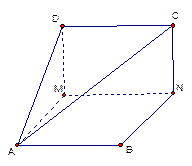
已知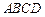 是边长为1的正方形,
是边长为1的正方形,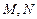 分别为
分别为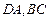 上的点,且
上的点,且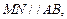 沿
沿 将正方形折成直二面角
将正方形折成直二面角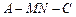 .
.
(I)求证:平面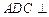 平面
平面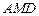 ;
;
(II)设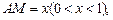 点
点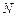 与平面
与平面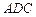 间的距离为
间的距离为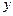 ,试用
,试用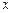 表示
表示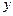 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为( )
| A.(3,0) | B.(-3,0) | C.(0,-3) | D.(0,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com