
已知函数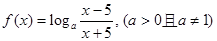 .
.
(1) 判断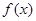 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2) 设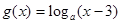 ,若方程
,若方程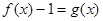 有实根,求
有实根,求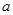 的取值范围;
的取值范围;
(3)是否存在实数m使得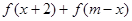 为常数?若存在,求出m的值;若不存在,说明理由.
为常数?若存在,求出m的值;若不存在,说明理由.
(1)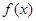 为奇函数;(2)
为奇函数;(2)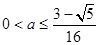 ;(3)存在-2.
;(3)存在-2.
【解析】第一问中利用奇偶函数定义进行判定,得到f(-x)=-f(x),所以说明
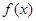 为奇函数
为奇函数
第二问中,因为方程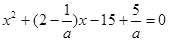 在
在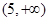 上有解
上有解
设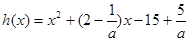 对称轴
对称轴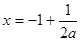
借助于二次函数得到。
第三问中,若存在这样的m,则
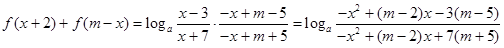
所以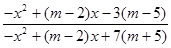 为常数,设
为常数,设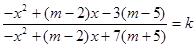
则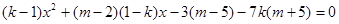 对定义域内的x恒成立
对定义域内的x恒成立
转化思想的运用。
解:(1)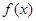 为奇函数
为奇函数
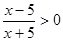 解得定义域为
解得定义域为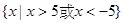 关于原点对称
关于原点对称
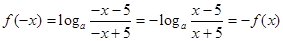 ,所以
,所以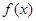 为奇函数
-------------4
为奇函数
-------------4
(2)方程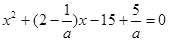 在
在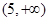 上有解
上有解
设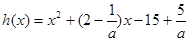 对称轴
对称轴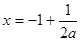
①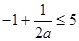 即
即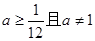 ,则
,则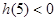 ,无解
,无解
②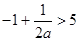 即
即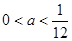 ,则
,则 解得
解得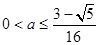
综上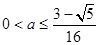 -------------10
-------------10
法二: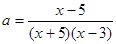 在
在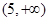 有解,设
有解,设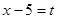 ,则
,则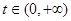
设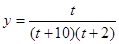 ,则
,则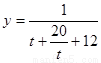 ,因为
,因为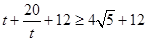 ,当且仅当
,当且仅当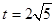 取“=“,所以
取“=“,所以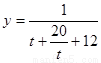 值域为
值域为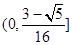 ,所以
,所以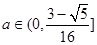
(3)若存在这样的m,则
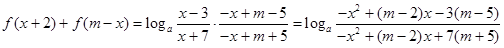
所以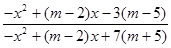 为常数,设
为常数,设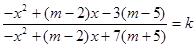
则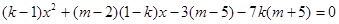 对定义域内的x恒成立
对定义域内的x恒成立
所以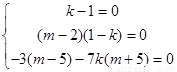 解得
解得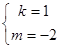
所以存在这样的m=-2 -----------16


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| x |
| lnx |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com