Question

【题目】下图是某校某班44名同学的某次考试的物理成绩y和数学成绩x的散点图：

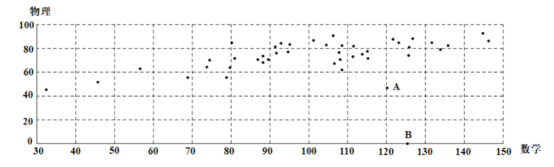
根据散点图可以看出y与x之间有线性相关关系，但图中有两个异常点A，B．经调查得知，A考生由于重感冒导致物理考试发挥失常，B生因故未能参加物理考试．为了使分析结果更科学准确，剔除这两组数据后，对剩下的数据作处理，得到一些统计量的值：

，，，，，其中，分别表示这42名同学的数学成绩、物理成绩，．y与x的相关系数．

（1）若不剔除A、B两名考生的数据，用44数据作回归分析，设此时y与x的相关系数为，试判断与r的大小关系，并说明理由；

（2）求y关于x的线性回归方程（系数精确到），并估计如果B考生参加了这次物理考试（已知B考生的数学成绩为125分），物理成绩是多少？（精确到个位）．

附：回归方程中，．

Answer 1

【答案】（1）；理由见解析；（2）；81分

【解析】

（1）结合散点图，可得出结论；

（2）利用题中给的相关系数，最小二乘法写出回归直线方程，再令x＝125，即可算出答案；

（1）．

理由如下：由图可知，y与x成正相关关系，

①异常点 A，B 会降低变量之间的线性相关程度．

②44个数据点与其回归直线的总偏差更大，回归效果更差，所以相关系数更小．

③42个数据点与其回归直线的总偏差更小，回归效果更好，所以相关系数更大．

④42个数据点更贴近其回归直线l．

⑤44个数据点与其回归直线更离散．

（以上理由写出任一个或其它言之有理均可得分）

（2）由题中数据可得：，，

所以，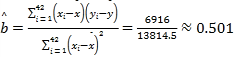

，

所以，

将代入，得，

所以估计B同学的物理成绩约为81分．