
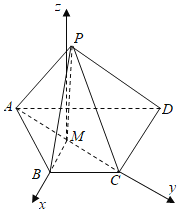
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
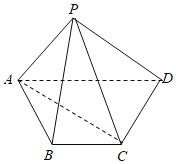
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(I)取![]() 的中点
的中点![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 平面
平面![]() 得出
得出![]() ;
;
(II)以![]() 为原点建立坐标系,求出平面
为原点建立坐标系,求出平面![]() 的法向量
的法向量![]() ,通过计算
,通过计算![]() 与
与![]() 的夹角得出
的夹角得出![]() 与平面
与平面![]() 所成角.
所成角.
(I)证明:取AC的中点M,连接PM,BM,
∵AB=BC,PA=PC,
∴AC⊥BM,AC⊥PM,又BM∩PM=M,
∴AC⊥平面PBM,
∵BP平面PBM,
∴AC⊥BP.
(II)解:∵底面ABCD是梯形.BC∥AD,AB=BC=CD=1,AD=2,
∴∠ABC=120°,
∵AB=BC=1,∴AC![]() ,BM
,BM![]() ,∴AC⊥CD,
,∴AC⊥CD,
又AC⊥BM,∴BM∥CD.
∵PA=PC![]() ,CM
,CM![]() ,∴PM
,∴PM![]() ,
,
∵PB![]() ,∴cos∠BMP
,∴cos∠BMP![]() ,∴∠PMB=120°,
,∴∠PMB=120°,
以M为原点,以MB,MC的方向为x轴,y轴的正方向,
以平面ABCD在M处的垂线为z轴建立坐标系
则A(0,![]() ,0),C(0,
,0),C(0,![]() ,0),P(
,0),P(![]() ,0,
,0,![]() ),D(﹣1,
),D(﹣1,![]() ,0),
,0),
∴![]() (﹣1,
(﹣1,![]() ,0),
,0),![]() (0,
(0,![]() ,0),
,0),![]() (
(![]() ,
,![]() ,
,![]() ),
),
设平面ACP的法向量为![]() (x,y,z),则
(x,y,z),则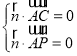 ,即
,即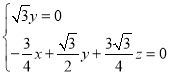 ,
,
令x![]() 得
得![]() (
(![]() ,0,1),
,0,1),
∴cos![]() ,
,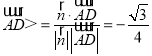 ,
,
∴直线AD与平面APC所成角的正弦值为|cos![]() ,
,![]() |
|![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,△ABC是以AC为斜边的等腰直角三角形,△BCD是等边三角形.如图②,将△BCD沿BC折起,使平面BCD⊥平面ABC,记BC的中点为E,BD的中点为M,点F、N在棱AC上,且AF=3CF,C![]() .
.
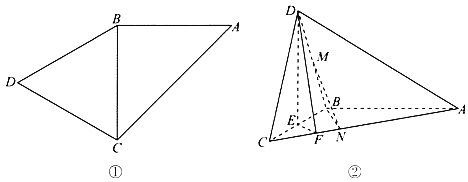
(1)试过直线MN作一平面,使它与平面DEF平行,并加以证明;
(2)记(1)中所作的平面为α,求平面α与平面BMN所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com