
已知函数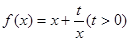 和点
和点 ,过点
,过点 作曲线
作曲线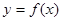 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.
(Ⅰ)设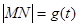 ,试求函数
,试求函数 的表达式;
的表达式;
(Ⅱ)是否存在 ,使得
,使得 、
、 与
与 三点共线.若存在,求出
三点共线.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数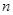 ,在区间
,在区间 内总存在
内总存在 个实数
个实数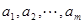 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
(Ⅰ)函数 的表达式为
的表达式为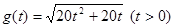 .
.
(Ⅱ)存在 ,使得点
,使得点 、
、 与
与 三点共线,且
三点共线,且 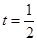 .
.
(Ⅲ) 的最大值为
的最大值为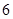 .
.
解析试题分析:(Ⅰ)设 、
、 两点的横坐标分别为
两点的横坐标分别为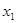 、
、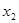 ,
, 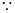
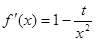 ,
,
∴切线 的方程为:
的方程为: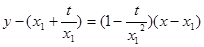 ,
,
又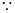 切线
切线 过点
过点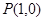 ,
, 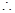 有
有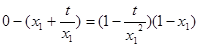 ,即
,即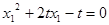 , (1)
, (1)
同理,由切线 也过点
也过点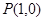 ,得
,得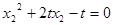 .(2)
.(2)
由(1)、(2),可得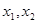 是方程
是方程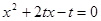 的两根,
的两根,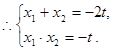 ( * )
( * )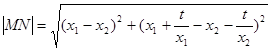
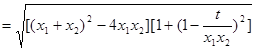 ,
,
把( * )式代入,得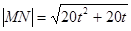 ,
,
因此,函数 的表达式为
的表达式为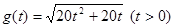 .
.
(Ⅱ)当点 、
、 与
与 共线时,
共线时,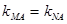 ,
,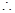
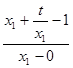 =
=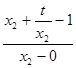 ,即
,即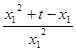 =
=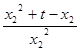 ,
,
化简,得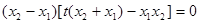 ,
,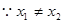 ,
,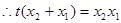 . (3)
. (3)
把(*)式代入(3),解得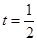 .
.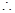 存在
存在 ,使得点
,使得点 、
、 与
与 三点共线,且
三点共线,且 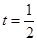 .
.
(Ⅲ)解法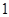 :易知
:易知 在区间
在区间 上为增函数,
上为增函数,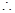
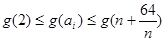
 ,
,
则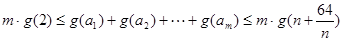 .
.
依题意,不等式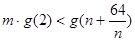 对一切的正整数
对一切的正整数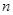 恒成立,
恒成立,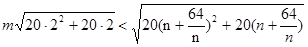 ,
,
即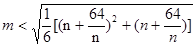 对一切的正整数
对一切的正整数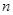 恒成立.
恒成立.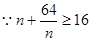 ,
, 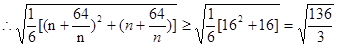 ,
,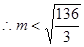 .
.
由于 为正整数,
为正整数,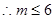 .
.
又当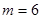 时,存在
时,存在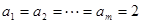 ,
,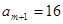 ,对所有的
,对所有的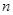 满足条件.
满足条件.
因此, 的最大值为
的最大值为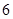 .
.
解法 :依题意,当区间
:依题意,当区间 的长度最小时,
的长度最小时,
得到的 最大值,即是所求值.
最大值,即是所求值.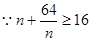 ,
,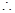 长度最小的区间为
长度最小的区间为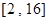
当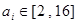
 时,与解法
时,与解法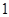


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
设函数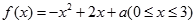 的最大值为
的最大值为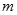 ,最小值为
,最小值为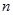 ,其中
,其中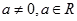 .
.
(1)求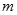 、
、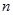 的值(用
的值(用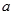 表示);
表示);
(2)已知角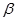 的顶点与平面直角坐标系
的顶点与平面直角坐标系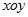 中的原点
中的原点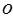 重合,始边与
重合,始边与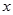 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点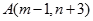 .求
.求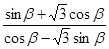 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度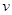 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度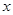 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当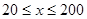 时,车流速度
时,车流速度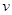 是车流密度
是车流密度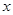 的一次函数.
的一次函数.
(Ⅰ)当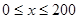 时,求函数
时,求函数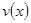 的表达式;
的表达式;
(Ⅱ)当车流密度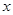 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)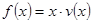 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后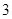 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第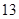 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款( ),试用
),试用 和
和 表示小王第
表示小王第 (
( )个月的还款额
)个月的还款额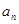 ;
;
(2)当 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月工资的余额是否能满足此月 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: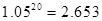 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈ ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人2002年底花100万元买了一套住房,其中首付30万元,70万元采用商业贷款.贷款的月利率为5‰,按复利计算,每月等额还贷一次,10年还清,并从贷款后的次月开始还贷.
(1)这个人每月应还贷多少元?
(2)为了抑制高房价,国家出台“国五条”,要求卖房时按照差额的20%缴税.如果这个人现在将住房150万元卖出,并且差额税由卖房人承担,问:卖房人将获利约多少元?(参考数据:(1+0.005)120≈1.8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com