
本小题满分10分)
已知直线l经过点P(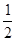 ,1),倾斜角
,1),倾斜角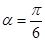 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为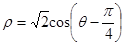 。
。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
已知动点 ,Q都在曲线C:
,Q都在曲线C: (β为参数)上,对应参数分别为
(β为参数)上,对应参数分别为
与 (0<
(0<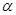 <2π),M为PQ的中点。
<2π),M为PQ的中点。
(Ⅰ)求M的轨迹的参数方程
(Ⅱ)将M到坐标原点的距离d表示为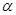 的函数,并判断M的轨迹是否过坐标原点。
的函数,并判断M的轨迹是否过坐标原点。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系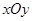 中,曲线
中,曲线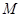 的参数方程为
的参数方程为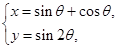 (
(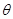 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点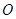 为极点,
为极点,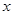 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线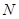 的极坐标方程为
的极坐标方程为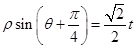 (其中
(其中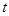 为常数).
为常数).
(1)若曲线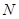 与曲线
与曲线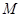 只有一个公共点,求
只有一个公共点,求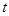 的取值范围;
的取值范围;
(2)当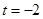 时,求曲线
时,求曲线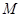 上的点与曲线
上的点与曲线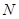 上的点的最小距离.
上的点的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
在平面直角坐标系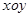 中,直线
中,直线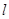 的参数方程为
的参数方程为 (t为参数,α为直线
(t为参数,α为直线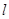 的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(1) 若直线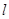 与圆C相切,求
与圆C相切,求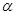 的值;
的值;
(2) 若 直线
直线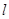 与圆C交与A,B两点,求
与圆C交与A,B两点,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出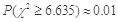 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( ).
| A.r2<r4<0<r3<r1 | B.r4<r2<0<r1<r3 | C.r4<r2<0<r3<r1 | D.r2<r4<0<r1<r3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com