
【题目】已知函数![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数)
为自然对数的底数)
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)见解析;(Ⅱ)1.
【解析】试题分析:(1)求出![]() 的导数,讨论当
的导数,讨论当![]() 时,
时, ![]() ,
, ![]() 无极值;当
无极值;当![]() 时,由
时,由![]() ,得
,得![]() ,求得单调区间,可得
,求得单调区间,可得![]() 在
在![]() 处取到极小值,且极小值为
处取到极小值,且极小值为![]() ,无极大值;(2)令
,无极大值;(2)令![]() ,则直线
,则直线![]() 与曲线
与曲线![]() 没有公共点方程
没有公共点方程![]() 在
在![]() 上没有实数解,分
上没有实数解,分![]() 与
与![]() 讨论即可得答案.
讨论即可得答案.
试题解析:(Ⅰ) ![]()
(ⅰ)当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为增函数,所以函数
上为增函数,所以函数![]() 无极值;
无极值;
(ⅱ)当![]() 时,
时, ![]() ,得
,得![]()
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)当![]() 时,
时, ![]()
令![]()
则若直线![]() 与曲线
与曲线![]() 没有公共点,等价于方程
没有公共点,等价于方程![]() 在
在![]() 上没有实数根
上没有实数根
当![]() 时,
时, 
又函数![]() 的图象在定义域
的图象在定义域![]() 上连续,可知方程
上连续,可知方程![]() 在
在![]() 上至少有一实数根,与方程
上至少有一实数根,与方程![]() 在
在![]() 上没有实数根矛盾,故
上没有实数根矛盾,故![]()
当![]() 时,
时, ![]() ,知方程
,知方程![]() 在
在![]() 上没有实数根
上没有实数根
所以![]() 的最大值为1.
的最大值为1.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点.若点
两点.若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某天数学课上,你突然惊醒,发现黑板上有如下内容:
例:求x3﹣3x,x∈[0,+∞)的最小值.解:利用基本不等式a+b+c≥3 ![]() ,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,当且仅当x=1时,取到最小值﹣2
,得到x3+1+1≥3x,于是x3﹣3x=x3+1+1﹣3x﹣2≥3x﹣3x﹣2=﹣2,当且仅当x=1时,取到最小值﹣2
(1)老师请你模仿例题,研究x4﹣4x,x∈[0,+∞)上的最小值;
(提示:a+b+c+d≥4 ![]() )
)
(2)研究 ![]() x3﹣3x,x∈[0,+∞)上的最小值;
x3﹣3x,x∈[0,+∞)上的最小值;
(3)求出当a>0时,x3﹣ax,x∈[0,+∞)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知左焦点为F(﹣1,0)的椭圆过点E(1, ![]() ).过点P(1,1)分别作斜率为k1 , k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1 , k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
(1)求椭圆的标准方程;
(2)若P为线段AB的中点,求k1;
(3)若k1+k2=1,求证直线MN恒过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
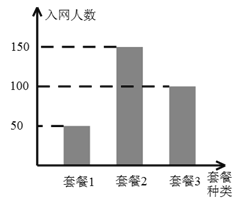
【题目】移动公司在春节正月初八这天推出4G套餐,对这天办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元. 初八当天参与活动的人数统计结果如图所示,
(Ⅰ)从参加当天活动的人中任选一人,求此人获得优惠金额不低于300元的概率(将频率视为概率);
(Ⅱ)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选两人,求这两人获得相等优惠金额的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽马鞍山二模】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
(Ⅰ)求直线![]() 与曲线C围成的区域面积;
与曲线C围成的区域面积;
(Ⅱ)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线C的切线
作曲线C的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若f(log2a)+f(2log ![]() a)≥2f(﹣1),则实数a的取值范围是 .
a)≥2f(﹣1),则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com