
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
【答案】
(1)解:根据平均数的个数可得75= ![]() ,
,
∴x6=90,
这六位同学的方差是 ![]() (25+1+9+25+9+225)=49,
(25+1+9+25+9+225)=49,
∴这六位同学的标准差是7
(2)解:由题意知本题是一个古典概型,
试验发生包含的事件是从5位同学中选2个,共有C52=10种结果,
满足条件的事件是恰有一位成绩在区间(68,75)中,共有C41=4种结果,
根据古典概型概率个数得到P= ![]() =0.4.
=0.4.
【解析】(1)根据平均数公式写出这组数据的平均数表示式,在表示式中有一个未知量,根据解方程的思想得到结果,求出这组数据的方差,再进一步做出标准差.(2)本题是一个古典概型,试验发生包含的事件是从5位同学中选2个,共有C52种结果,满足条件的事件是恰有一位成绩在区间(68,75)中,共有C41种结果,根据概率公式得到结果.


科目:高中数学 来源: 题型:
【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
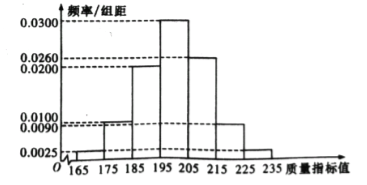
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B,C,D是直角坐标系中不同的四点,若 ![]() =λ
=λ ![]() (λ∈R),
(λ∈R), ![]() =μ
=μ ![]() (μ∈R),且
(μ∈R),且 ![]() =2,则下列说法正确的是( )
=2,则下列说法正确的是( )
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C,D可能同时在线段AB上
D.C,D不可能同时在线段AB的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x轴、y轴正方向上的单位向量分别是 ![]() 、
、 ![]() ,坐标平面上点列An、Bn(n∈N*)分别满足下列两个条件:①
,坐标平面上点列An、Bn(n∈N*)分别满足下列两个条件:① ![]() =
= ![]() 且
且 ![]() =
= ![]() +
+ ![]() ;②
;② ![]() =4
=4 ![]() 且
且 ![]() =
= ![]() ×4
×4 ![]() ;
;
(1)写出 ![]() 及
及 ![]() 的坐标,并求出
的坐标,并求出 ![]() 的坐标;
的坐标;
(2)若△OAnBn+1的面积是an , 求an(n∈N*)的表达式;
(3)对于(2)中的an , 是否存在最大的自然数M,对一切n∈N*都有an≥M成立?若存在,求出M,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通二模19】已知函数![]() ,
,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数![]() 在x
在x![]() 1处的切线方程;
1处的切线方程;
(2)若存在![]()
![]() ,使得
,使得![]() 成立,其中
成立,其中![]() 为常数,
为常数,
求证:![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
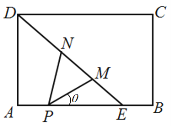
【题目】【2017扬州一模】如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com