
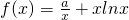 ,g(x)=x3-x2-3,
,g(x)=x3-x2-3,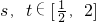 ,都有f(s)≥g(t)成立.
,都有f(s)≥g(t)成立. +xlnx,f'(x)=-
+xlnx,f'(x)=- +lnx+1,
+lnx+1, )
) )时,g'(x)<0,当x∈(
)时,g'(x)<0,当x∈( ,2)时,g'(x)>0,
,2)时,g'(x)>0, )=-
)=-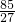 ,g(x)max=g(2)=1
,g(x)max=g(2)=1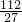
 ,2]上,g(x)的最大值为g(2)=1
,2]上,g(x)的最大值为g(2)=1 ,2],
,2],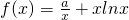 ≥
≥ +xlnx,
+xlnx, +xlnx,h'(x)=-
+xlnx,h'(x)=- +lnx+1,h'(1)=0
+lnx+1,h'(1)=0 ,1),h'(x)<0,当x∈(1,2],h'(x)>0
,1),h'(x)<0,当x∈(1,2],h'(x)>0 +xlnx在区间[
+xlnx在区间[ ,1)上递减,在区间(1,2]上递增,
,1)上递减,在区间(1,2]上递增, ,2],f(x)≥1成立,
,2],f(x)≥1成立,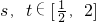 ,都有f(s)≥g(t)成立.
,都有f(s)≥g(t)成立. +xlnx,根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成斜截式即可.
+xlnx,根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成斜截式即可. ,2]上,g(x)的最大值,然后求出h(x)的最小值,从而证明出在区间[
,2]上,g(x)的最大值,然后求出h(x)的最小值,从而证明出在区间[ ,2]上f(x)≥g(x)恒成立,从而得到结论.
,2]上f(x)≥g(x)恒成立,从而得到结论.

科目:高中数学 来源: 题型:
| x2+ax+1 | x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 符号[x]表示不超过x的最大整数,如[2]=2,[π]=3,[-
符号[x]表示不超过x的最大整数,如[2]=2,[π]=3,[-| 2 |
| x |
| 3 |
| ∫ | b a |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省丽水中学高三(下)第一次月考数学试卷(理科)(解析版) 题型:解答题
 ,g(x)=x3-x2-3.
,g(x)=x3-x2-3. ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市学军中学高考数学模拟试卷(理科)(解析版) 题型:解答题
 ,g(x)=x3-x2-3.
,g(x)=x3-x2-3. ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com