
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
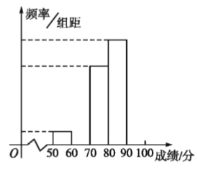
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 8 | 0.16 |
| 10 | ________ |
| ________ | ________ |
| 14 | 0.28 |
合计 | ________ | 1.00 |
(2)请你估算该年级学生成绩的中位数;
(3)如果用分层抽样的方法从样本分数在![]() 和
和![]() 的人中共抽取6人,再从6人中选2人,求2人分数都在
的人中共抽取6人,再从6人中选2人,求2人分数都在![]() 的概率.
的概率.
【答案】(1)见解析;(2)83.125;(3)![]() .
.
【解析】
(1)先填写完整频率分布表,由此补全频率分布直方图;
(2)设中位数为,利用频率分布直方图列出方程,求出中位数;
(3)由题意可知样本分数在![]() 有8人,样本分数在
有8人,样本分数在![]() 有16人,用分层抽样的方法从样本分数在
有16人,用分层抽样的方法从样本分数在![]() 和
和![]() 的人中共抽取6人,则抽取的分数在
的人中共抽取6人,则抽取的分数在![]() 和
和![]() 的人数分别为2人和4人,记分数在
的人数分别为2人和4人,记分数在![]() 为
为![]() ,在
,在![]() 的为
的为![]() ,由此利用列举法能求出2人分数在
,由此利用列举法能求出2人分数在![]() 的概率.
的概率.
解:(1)填写频率分布表中的空格,如下表:
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 8 | 0.16 |
| 10 | 0.2 |
| 16 | 0.32 |
| 14 | 0.28 |
合计 | 50 | 1.00 |
补全频率分布直方图,如下图:
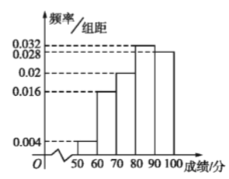
(2)设中位数为x,依题意得![]() ,
,
解得![]() ,所以中位数约为83.125.
,所以中位数约为83.125.
(3)由题意知样本分数在![]() 有8人,样本分数在
有8人,样本分数在![]() 有16人,
有16人,
用分层抽样的方法从样本分数在![]() 和
和![]() 的人中共抽取6人,
的人中共抽取6人,
则抽取的分数在![]() 和
和![]() 的人数分别为2人和4人.
的人数分别为2人和4人.
记分数在![]() 的为
的为![]()
![]() ,在
,在![]() 的为
的为![]()
![]()
![]()
![]() .
.
从已抽取的6人中任选两人的所有可能结果有15种,分别为
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
设“2人分数都在![]() ”为事件A,
”为事件A,
则事件A包括![]()
![]()
![]()
![]()
![]()
![]() 共6种,
共6种,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-(a+1)x+alnx+1
x2-(a+1)x+alnx+1
(Ⅰ)若x=3是f(x)的极值点,求f(x)的极大值;
(Ⅱ)求a的范围,使得f(x)≥1恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有15个省三好学生名额分给1、2、3、4共四个班级,其中1班至少2个名额,2班、4班每班至少3个名额,3班最多2个名额,则共有_________种不同分配方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
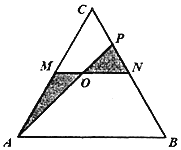
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com