
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设函数![]() ,当
,当![]() 时,若
时,若![]() ,
,![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)求出导函数![]() ,然后根据导函数的符号判断出函数的单调性.(2)由题意可得问题等价于“
,然后根据导函数的符号判断出函数的单调性.(2)由题意可得问题等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”.所以分别求出函数
上的最大值”.所以分别求出函数![]() 在
在![]() 上的最大值和函数
上的最大值和函数![]() 在
在![]() 上的最大值,根据题意建立不等式组,解不等式组可得所求结果.
上的最大值,根据题意建立不等式组,解不等式组可得所求结果.
(1)∵![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,
若![]() ,则
,则![]() 单调递减;若
单调递减;若![]() ,则
,则![]() 单调递增.
单调递增.
综上可得,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减.
单调递减.
∴当![]() 时,
时,![]() .
.
又![]() 在
在![]() 上的最大值为
上的最大值为![]() 中的较大者.
中的较大者.
由题意得“![]() ,
,![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”,
上的最大值”,
∴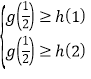 ,即
,即![]() ,解得
,解得![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆E经过M(﹣1,0),N(0,1),P(![]() ,
,![]() )三点.
)三点.
(1)求圆E的方程;
(2)若过点C(2,2)作圆E的两条切线,切点分别是A,B,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点C在直线3x﹣y=0上,顶点A、B的坐标分别为(4,2),(0,5).
(Ⅰ)求过点A且在x,y轴上的截距相等的直线方程;
(Ⅱ)若△ABC的面积为10,求顶点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,斜率为1的直线l交椭圆于A、B两点,且线段AB的中点坐标为
,斜率为1的直线l交椭圆于A、B两点,且线段AB的中点坐标为![]() .
.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 若P是椭圆与双曲线
若P是椭圆与双曲线![]() 在第一象限的交点,求
在第一象限的交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月25日,平昌冬奥会闭幕式上的“北京8分钟”惊艳了世界。我们学校为了让我们更好的了解奥运,了解新时代祖国的科技发展,在高二年级举办了一次知识问答比赛。比赛共设三关,第一、二关各有两个问题,两个问题全答对,可进入下一关;第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得分别为1、2、3分的积分奖励,高二、一班对三关中每个问题回答正确的概率依次为![]() ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)记![]() 表示事件“高二、一班未闯到第三关”,求
表示事件“高二、一班未闯到第三关”,求![]() 的值;
的值;
(2)记![]() 表示高二、一班所获得的积分总数,求
表示高二、一班所获得的积分总数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com