
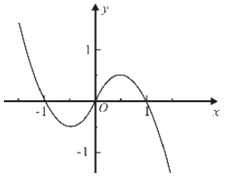
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1﹣x).
(1)在如图所给直角坐标系中画出函数f(x)的草图,并直接写出函数f(x)的零点;
(2)求出函数f(x)的解析式.
【答案】解:(1)当x≥0时,由f(x)=2x(1﹣x)=0得x=0或x=1,
∵f(x)是定义在R上的奇函数,
∴当x<0时,函数的零点为﹣1,
即函数f(x)的零点为0,﹣1,1.
(2)若x<0,则﹣x>0,
∵x≥0时,f(x)=2x(1﹣x).
∴当﹣x>0时,f(﹣x)=﹣2x(1+x).
∵f(x)是定义在R上的奇函数,
∴f(﹣x)=﹣2x(1+x)=﹣f(x),
即f(x)=2x(1+x),x<0.
即f(x)=![]() .
.
【解析】(1)根据函数奇偶性的性质以及函数零点的定义进行求解即可.
(2)根据函数奇偶性的性质进行转化求解即可.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°, 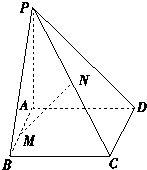
(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1 , x2 , …,xn , 有 ![]() ≤f(
≤f( ![]() ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某问答游戏的规则是:共5道选择题,基础分为50分,每答错一道题扣10分,答对不扣分.试分别用列表法、图象法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入)
问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b(a,b∈R),
(1)若函数f(x)在区间[﹣1,1]上不单调,求实数a的取值范围;
(2)记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,证明:当|a|≥2时,M(a,b)≥2.
查看答案和解析>>
科目:高中数学 来源: 题型:
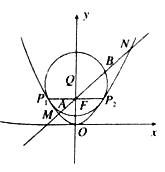
【题目】如图,抛物线![]() 的准线为
的准线为![]() ,取过焦点
,取过焦点![]() 且平行于
且平行于![]() 轴的直线与抛物线交于不同的两点
轴的直线与抛物线交于不同的两点![]() ,过
,过![]() 作圆心为
作圆心为![]() 的圆,使抛物线上其余点均在圆外,且
的圆,使抛物线上其余点均在圆外,且![]() .
.
(Ⅰ)求抛物线![]() 和圆
和圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com