
【题目】已知函数f(x)=x2+ax+b(a,b∈R),
(1)若函数f(x)在区间[﹣1,1]上不单调,求实数a的取值范围;
(2)记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,证明:当|a|≥2时,M(a,b)≥2.
【答案】
(1)解:由题意知:
函数f(x)的对称轴为x= ![]()
∵函数f(x)在区间[﹣1,1]上不单调,
∴ ![]() ∈[﹣1,1]
∈[﹣1,1]
∴a∈[﹣2,2])
(2)解:由|a|≥2得:a≥2,或a≤﹣2,
而函数f(x)的对称轴为直线x= ![]() ,
,
M(a,b)=|f(x)|max=max{|f(﹣1)|,|f(1)|}= ![]()
则4≤2|a|≤|1+a+b|+|1﹣a+b|≤2M(a,b)
即M(a,b)≥2)
【解析】(1)若函数f(x)在区间[﹣1,1]上不单调,则函数图象的对称轴x= ![]() ∈[﹣1,1],解得答案;(2)由|a|≥2得:a≥2,或a≤﹣2,则M(a,b)=|f(x)|max=max{|f(﹣1)|,|f(1)|}=
∈[﹣1,1],解得答案;(2)由|a|≥2得:a≥2,或a≤﹣2,则M(a,b)=|f(x)|max=max{|f(﹣1)|,|f(1)|}= ![]() ,进而可证得M(a,b)≥2.
,进而可证得M(a,b)≥2.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为检验寒假学生自主学习的效果,年级部对某班50名学生各科的检测成绩进行了统计,下面是政治成绩的频率分布直方图,其中成绩分组区间是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求图中的![]() 值及平均成绩;
值及平均成绩;
(2)从分数在![]() 中选5人记为
中选5人记为![]() ,从分数在
,从分数在![]() 中选3人,记为
中选3人,记为![]() ,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求
,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1﹣x).
(1)在如图所给直角坐标系中画出函数f(x)的草图,并直接写出函数f(x)的零点;
(2)求出函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用简单随机抽样方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个体a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)的定义域为[﹣4,0)∪(0,4],若当x∈(0,4]时,f(x)=log2x,
(1)求出函数在定义域[﹣4,0)∪(0,4]的解析式;
(2)求不等式xf(x)<0得解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017西安铁一中五模】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 上总存在相异两点
上总存在相异两点![]() ,使曲线
,使曲线![]() 在
在![]() 两点处的切线互相平行,试求
两点处的切线互相平行,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线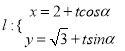
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ![]() ,3]
,3]
D.(0, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com