
【题目】过抛物线![]() )的焦点F且斜率为
)的焦点F且斜率为![]() 的直线交抛物线C于M,N两点,且
的直线交抛物线C于M,N两点,且![]() .
.
(1)求p的值;
(2)抛物线C上一点![]() ,直线
,直线![]() (其中
(其中![]() )与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为
)与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为![]() ,
,![]() .直线l是否过定点?如果是,请求出所有定点;如果不是,请说明理由;
.直线l是否过定点?如果是,请求出所有定点;如果不是,请说明理由;
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
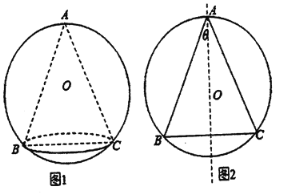
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏公司对今年新开发的一些游戏进行评测,为了了解玩家对游戏的体验感,研究人员随机调查了300名玩家,对他们的游戏体验感进行测评,并将所得数据统计如图所示,其中![]() .
.
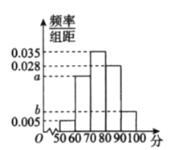
(1)求这300名玩家测评分数的平均数;
(2)由于该公司近年来生产的游戏体验感较差,公司计划聘请3位游戏专家对游戏进行初测,如果3人中有2人或3人认为游戏需要改进,则公司将回收该款游戏进行改进;若3人中仅1人认为游戏需要改进,则公司将另外聘请2位专家二测,二测时,2人中至少有1人认为游戏需要改进的话,公司则将对该款游戏进行回收改进.已知该公司每款游戏被每位专家认为需要改进的概率为![]() ,且每款游戏之间改进与否相互独立.
,且每款游戏之间改进与否相互独立.
(i)对该公司的任意一款游戏进行检测,求该款游戏需要改进的概率;
(ii)每款游戏聘请专家测试的费用均为300元/人,今年所有游戏的研发总费用为50万元,现对该公司今年研发的600款游戏都进行检测,假设公司的预算为110万元,判断这600款游戏所需的最高费用是否超过预算,并通过计算说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了
内为优质品.从两个企业生产的零件中各随机抽出了![]() 件,测量这些零件的质量指标值,得结果如下表:
件,测量这些零件的质量指标值,得结果如下表:
甲企业:
分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
| 5 |
乙企业:
分组 |
|
|
|
|
|
|
|
频数 | 5 |
|
|
|
|
| 5 |
(1)已知甲企业的![]() 件零件质量指标值的样本方差
件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值X服从正态分布
,该企业生产的零件质量指标值X服从正态分布![]() ,其中μ近似为质量指标值的样本平均数
,其中μ近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组中的数据用该组区间的中点值作代表),
时,同一组中的数据用该组区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据企业的抽样数据,估计所生产的零件中,质量指标值不低于
,试根据企业的抽样数据,估计所生产的零件中,质量指标值不低于![]() 的产品的概率.(精确到
的产品的概率.(精确到![]() )
)
(2)由以上统计数据完成下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为两个企业生产的零件的质量有差异.
的前提下认为两个企业生产的零件的质量有差异.
甲厂 | 乙厂 | 总计 | |
优质品 | |||
非优质品 | |||
总计 |
附:
参考数据:![]() ,
,
参考公式:若![]() ,则
,则![]() ,
,
![]() ,
,![]() ;
;

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三条边长,则下列结论中正确的是( )
的三条边长,则下列结论中正确的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三条边
不能构成一个三角形的三条边
②对一切![]() ,都有
,都有![]()
③若![]() 为钝角三角形,则存在
为钝角三角形,则存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com