
 ”的概率是.
”的概率是.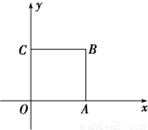
 的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于
的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于 ”的概率
”的概率 .(6分)
.(6分) ,
, ,
, 后剩余的正方形,
后剩余的正方形, ×
× =
= ,
, .(12分)
.(12分)

科目:高中数学 来源: 题型:
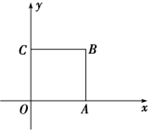 如图,正方形OABC的边长为2.
如图,正方形OABC的边长为2.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
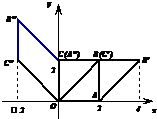 (Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
(Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
|
| π |
| 4 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012人教A版高中数学必修三3.3几何概型练习题(一)(解析版) 题型:填空题
如图,正方形OABC的边长为2.
(1)在其四边或内部取点P(x,y),且x,y∈Z,则事件“|OP|>1”的概率________.
(2)在其内部取点P(x,y),且x,y∈R,则事件“△POA,△PAB,△PBC,△PCO的面积均大于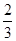 ”的概率是________.
”的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com