
【题目】为迎接2018年省运会,宁德市某体育馆需要重新铺设塑胶跑道.已知每毫米厚的跑道的铺设成本为10万元,跑道平均每年的维护费C(单位:万元)与跑道厚度x(单位:毫米)的关系为C(x)=![]() ,x∈[10,15].若跑道厚度为10毫米,则平均每年的维护费需要9万元.设总费用f(x)为跑道铺设费用与10年维护费之和.
,x∈[10,15].若跑道厚度为10毫米,则平均每年的维护费需要9万元.设总费用f(x)为跑道铺设费用与10年维护费之和.
(1)求k的值与总费用f(x)的表达式;
(2)塑胶跑道铺设多厚时,总费用f(x)最小,并求最小值.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数
为参数![]() 以原点为极点x轴正半轴为极轴建立极坐标系,直线
以原点为极点x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业(以下简称外卖甲,外卖乙)的经营情况进行了调查,调查结果如表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单 | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单 | 2.2 | 2.3 | 10 | 5 | 15 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(ⅰ)请用相关系数![]() 加以说明:(若
加以说明:(若![]() ,则可认为
,则可认为![]() 与
与![]() 有较强的线性相关关系(
有较强的线性相关关系(![]() 值精确到0.001))
值精确到0.001))
(ⅱ)经计算求得![]() 与
与![]() 之间的回归方程为
之间的回归方程为![]() .假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(
.假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围:(![]() 值精确到0.01)
值精确到0.01)
(2)试根据表格中这五天的日接单量情况,从平均值和方差角度说明这两家外卖企业的经营状况.
相关公式:相关系数 ,
,
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P为椭圆C上一点,且PF2垂直于x轴,连结PF1并延长交椭圆于另一点Q,设
(a>b>0)的左、右焦点分别为F1,F2,P为椭圆C上一点,且PF2垂直于x轴,连结PF1并延长交椭圆于另一点Q,设![]() =λ
=λ![]() .
.

(1)若点P的坐标为(2,3),求椭圆C的方程及λ的值;
(2)若4≤λ≤5,求椭圆C的离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心为坐标原点,左焦点为F1(﹣1,0),离心率
的中心为坐标原点,左焦点为F1(﹣1,0),离心率![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,如图所示.
,如图所示.

①证明:![]() ;
;
②求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 满足:
满足: ![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),证明:直线
不重合),证明:直线![]() 恒过定点,并求该定点的坐标.
恒过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 的直线
的直线![]() 与中心在原点,焦点在
与中心在原点,焦点在![]() 轴上且离心率为
轴上且离心率为![]() 的椭圆
的椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 过线段
过线段![]() 的中点,同时椭圆
的中点,同时椭圆![]() 上存在一点与右焦点关于直线
上存在一点与右焦点关于直线![]() 对称.
对称.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
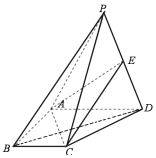
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com