
设数列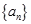 的前n项和为
的前n项和为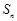 ,且满足
,且满足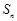 =2-
=2-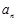 ,
,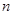 =1,2,3,….
=1,2,3,….
(1)求数列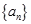 的通项公式;
的通项公式;
(2)若数列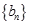 满足
满足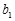 =1,且
=1,且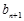 =
=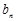 +
+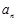 ,求数列
,求数列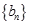 的通项公式;
的通项公式;
(3)设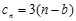 ,求数列
,求数列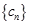 的前
的前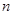 项和为
项和为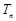 .
.
(1) =
= ( n∈
( n∈ )(2)
)(2) =
= (
( =1,2,3,…)
=1,2,3,…)
(3) 8-
8-
【解析】
试题分析:(1)因为 =1时,
=1时, +
+ =
= +
+ =2,所以
=2,所以 =1.
=1.
因为 =2-
=2- ,即
,即 +
+ =2,所以
=2,所以 +
+ =2.
=2.
两式相减: -
- +
+ -
- =0,即
=0,即 -
- +
+ =0,故有
=0,故有 =
= .
.
因为 ≠0,所以
≠0,所以 =
= ( n∈
( n∈ ).
).
所以数列 是首项
是首项 =1,公比为
=1,公比为 的等比数列,
的等比数列,
所以 =
= (
(  ∈
∈ ).
……5分
).
……5分
(2)因为 =
= +
+ ( n=1,2,3,…),所以
( n=1,2,3,…),所以 -
- =
= .从而有
.从而有
 =1,
=1, =
= ,
, =
= ,…,
,…, =
= (
(  =2,3,…).
=2,3,…).
将这 -1个等式相加,得
-1个等式相加,得
 -
- =1+
=1+ +
+ +…+
+…+ =
= =2-
=2- .(
.( =2,3,…).
=2,3,…).
又因为 =1,所以
=1,所以 =3-
=3- (
(  =2,3,…).
=2,3,…).
经检验,对 =1也成立,
=1也成立,
故 =3-
=3- =
= (
( =1,2,3,…).
……10分
=1,2,3,…).
……10分
(3)因为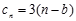 =
= ,
,
所以 =
= . ①
. ①
 =
= . ②
. ②
①-②,得 =
= -
- .
.
故 =
= -
- =8-
=8- -
- =8-
=8- ( n=1,2,3,…).
( n=1,2,3,…).
……15分
考点:本小题主要考查由递推关系式求数列的通项公式、等差等比数列的通项公式和错位相减法求数列的前n项的和,考查了学生对基础知识的掌握和灵活应用能力以及运算求解能力.
点评:一般解数列的解答题时会给出一个递推关系式,此时一般情况下会再写一个作差,写的时候要特别注意首项是否能取到,另外错位相减法求和是高考中常考的内容,要多加练习.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2n |
| an |
| 4n-1 |
| 2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a22 |
| 1 |
| a2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 2011 |
| 2012 |
查看答案和解析>>
科目:高中数学 来源:2011届广西省桂林中学高三11月月考数学文卷 题型:解答题
(本小题满分12分)设数列 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,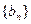 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 和
和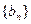 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com