
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 与
与![]() 的图象有两个不同的交点
的图象有两个不同的交点![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,在
时,在![]() 递增;当
递增;当![]() 时,递增区间为
时,递增区间为![]() ,递减为
,递减为![]() ;(2)
;(2)![]() .
.
【解析】
(1)求得![]() ,分类讨论,根据导函数的符号,即可求得函数的单调区间;
,分类讨论,根据导函数的符号,即可求得函数的单调区间;
(2)函数![]() 与
与![]() 有两个不同的交点转化为函数
有两个不同的交点转化为函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,当
,当![]() 时,利用函数
时,利用函数![]() 单调性与最值,构造
单调性与最值,构造![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性和最值,即可求解.
的单调性和最值,即可求解.
(1)由函数![]() ,
,![]() ,
,
可得![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,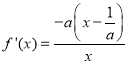 ,
,
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
∴函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减为
,单调递减为![]() ,
,
综上可得:当![]() 时,函数
时,函数![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减为
,单调递减为![]() .
.
(2)函数![]() 与
与![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() ,其中
,其中![]() ,
,
等价于函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,其中
,其中![]() .
.
由(Ⅰ)知,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数,不可能有两个零点,
上是增函数,不可能有两个零点,
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
此时![]() 为函数
为函数![]() 的最大值,
的最大值,
当![]() 时,
时,![]() 最多有一个零点,∴
最多有一个零点,∴![]() ,解得
,解得![]() ,
,
此时,![]() ,且
,且![]() ,
,
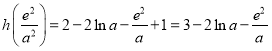 ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即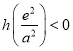 ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在多边形![]() 中(图1).四边形
中(图1).四边形![]() 为长方形,
为长方形,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,现以
,现以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 内的射影恰好是
内的射影恰好是![]() 的中点(图2).
的中点(图2).
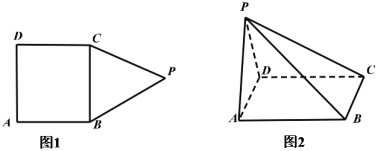
(1)证明:![]() 平面
平面![]() :
:
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 是以
是以![]() 为直径的圆上的动点(异于
为直径的圆上的动点(异于![]() ,
,![]() ),已知
),已知![]() ,
,![]() ,
,![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
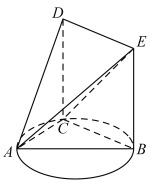
(1)求证:![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
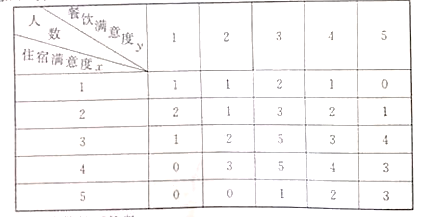
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,![]() .
.
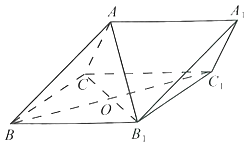
(1)求证:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且点A在侧面BB1C1C上的投影为点O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com