
【题目】已知函数![]() .
.
(1)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相切,求直线
相切,求直线![]() 的斜率的值;
的斜率的值;
(2)设![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,设切点坐标为
,设切点坐标为![]() ,根据题意可得出关于
,根据题意可得出关于![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 的值,进而可得出
的值,进而可得出![]() 的值;
的值;
(2)根据题意知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,然后求得函数
,然后求得函数![]() 的导数,对实数
的导数,对实数![]() 的取值进行分类讨论,利用导数分析函数
的取值进行分类讨论,利用导数分析函数![]() 的单调性,验证条件“当
的单调性,验证条件“当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ”是否满足,由此可得出实数
”是否满足,由此可得出实数![]() 的取值范围.
的取值范围.
(1)因为直线![]() 过点
过点![]() ,不妨设直线
,不妨设直线![]() 的方程为
的方程为![]() ,由题意得
,由题意得![]() ,
,
设切点为![]() ,则
,则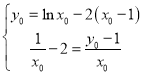 ,解得
,解得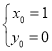 .
.
直线![]() 过点
过点![]() ,则有
,则有![]() ,解得
,解得![]() ,即直线
,即直线![]() 的斜率为
的斜率为![]() ;
;
(2)![]() ,
,![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
此时![]() ,即
,即![]() ,不合乎题意;
,不合乎题意;
②若![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
(i)当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
于是有![]() ;
;
(ii)当![]() 时,记
时,记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
此时![]() ,即
,即![]() ,不合乎题意;
,不合乎题意;
(iii)若![]() ,记
,记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
此时![]() ,即
,即![]() ,不合乎题意.
,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点为
)的右顶点为![]() .左、右焦点分别为
.左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆于点
轴的直线交椭圆于点![]() (
(![]() 在第象限),直线
在第象限),直线![]() 的斜率为
的斜率为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不与
不与![]() 、
、![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 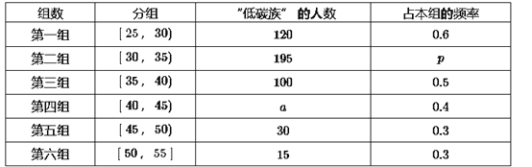
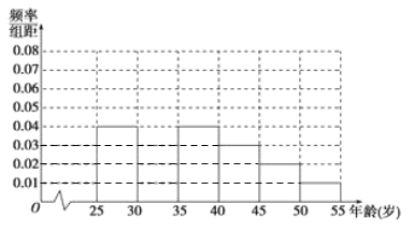
完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
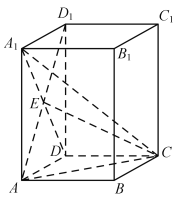
(1)证明:AE⊥平面ECD.
(2)求直线A1C与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
![]() 若
若![]() ,点K在椭圆E上,
,点K在椭圆E上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
![]() 证明:直线OM的斜率与l的斜率的乘积为定值;
证明:直线OM的斜率与l的斜率的乘积为定值;
![]() 若l过点
若l过点![]() ,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com