
【题目】如图,在多面体![]() 中,
中,![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,点M为棱
,点M为棱![]() 的中点.
的中点.
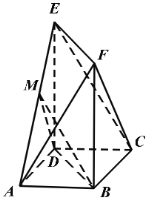
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() ,
,![]() ,求E点到平面
,求E点到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据条件证明四边形![]() 为平行四边形即可.
为平行四边形即可.
(2)设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 为
为![]() 的中点,由三角形中位线的性质可得
的中点,由三角形中位线的性质可得![]() 平面
平面![]() ,由面面垂直的性质定理可得
,由面面垂直的性质定理可得![]() ,则
,则![]() 平面
平面![]() .最后利用面面平行的判断定理可得平面
.最后利用面面平行的判断定理可得平面![]() 平面
平面![]() .
.
(3)连接![]() .由几何关系可证得AC⊥平面
.由几何关系可证得AC⊥平面![]() ,且垂足为
,且垂足为![]() , 则
, 则![]() ,由
,由![]() ,可求E点到平面
,可求E点到平面![]() 的距离.
的距离.
(1)证明:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]()
因为![]()
所以四边形![]() 为平行四边形
为平行四边形
所以![]()
(2)证明:

设![]() 与
与![]() 交于点N,则N为
交于点N,则N为![]() 的中点,
的中点,![]() 为
为![]() 的中位线,
的中位线,
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(3)解:连接![]() ,
,![]() .
.
在正方形![]() 中,
中,![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() ,且垂足为N,
,且垂足为N,
![]() ,
,
![]()
∴![]() ,
,
由![]() ,N是
,N是![]() 中点知,
中点知,![]() ,
,
在![]() 中,
中,
![]() ,
,
因为![]() ,
,
设E点到平面![]() 的距离为
的距离为![]() ,则
,则![]() .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
| 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 5 | 4 | 2 |
已知![]() 和
和![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润![]() 取到最大值?
取到最大值?
参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
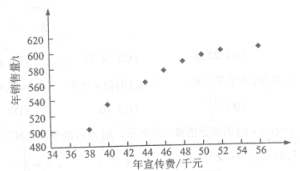
【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]()
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: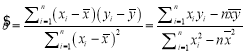 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com