
【题目】已知函数![]() ,
, ![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,令
时,令![]() ,其导函数为
,其导函数为![]() ,设
,设![]() 是函数
是函数![]() 的两个零点,判断
的两个零点,判断![]() 是否为
是否为![]() 的零点?并说明理由.
的零点?并说明理由.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先求函数导数,根据a的范围讨论导函数在定义区间上零点,根据导函数零点情况确定函数极值,(2)根据零点解得![]() ,代入
,代入![]() 得
得 . 构造函数
. 构造函数![]() ,其中
,其中![]() ,最后根据导数确定函数
,最后根据导数确定函数![]() 单调性,根据单调性确定函数
单调性,根据单调性确定函数![]() 无零点.
无零点.
试题解析:(1)依题意知函数![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,由
时,由![]() 得:
得: ![]() ,
,
则当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() 不是导函数
不是导函数![]() 的零点.
的零点.
证明如下:由(Ⅰ)知函数![]() .
.
∵![]() ,
, ![]() 是函数
是函数![]() 的两个零点,不妨设
的两个零点,不妨设![]() ,
,
∴![]() ,两式相减得:
,两式相减得: ![]()
即: ![]()
又![]() .
.
则![]()
 .
.
设![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,
,  .
.
又![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是増函数,
上是増函数,
则![]() ,即当
,即当![]() 时,
时, ![]() ,
,
从而![]() ,
,
又![]() 所以
所以 ,
,
故![]() ,所以
,所以![]() 不是导函数
不是导函数![]() 的零点.
的零点.


科目:高中数学 来源: 题型:
【题目】历史数据显示:某城市在每年的3月11日—3月15日的每天平均气温只可能是-5℃,-6℃,-7℃,-8℃中的一个,且等可能出现.
(Ⅰ)求该城市在3月11日—3月15日这5天中,恰好出现两次-5℃,一次-8℃的概率;
(Ⅱ)若该城市的某热饮店,随平均气温的变化所售热饮杯数如下表
平均气温t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯数y | 19 | 22 | 24 | 27 |
根据以上数据,求![]() 关于
关于![]() 的线性回归直线方程.
的线性回归直线方程.
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某市骑行过共享单车的人数约占全市的80%,为确定单车的投放数量以及对同年龄的车型配比,需要对该市市民每月骑行单车的次数进行统计,如表所示是对该市随机抽取100位市民的调查结果,每月骑行次数不超过20次称“不经常骑行”,超过20次称“经常骑行”.
经常骑行 | 不经常骑行 | 合计 | |
年龄不低于40岁 | 15 | 25 | 40 |
年龄低于40岁 | 35 | 25 | 60 |
合计 | 50 | 50 | 100 |
(1)是否有95%的把握认为骑行单车次数与年龄有关?
(2)以样本的频率为概率
①现从该市市民中随机抽取1人,求该人为“经常骑行”的概率
②已知该市人口约为600万,忽略把经常骑行人数的骑行次数,统计得经常骑行人群每人每月骑行次数的平均值为45次(每月按30天计算),若每辆单车每天被骑行(15次左右,可达到既缓解交通压力又减少了胡乱放置的目的,则该市配置单车的数量应为多少?
附参考公式及数据![]()
| 0.10 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】支付宝和微信支付是目前市场占有率较高的支付方式,某第三方调研机构对使用这两种支付方式的人数作了对比.从全国随机抽取了100个地区作为研究样本,计算了各个地区样本的使用人数,其频率分布直方图如图.
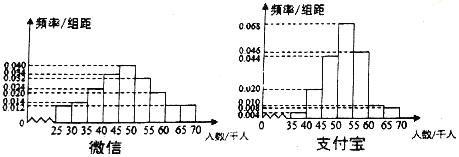
(1)记A表示事件“微信支付人数低于50千人”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为支付人数与支付方式有关;
支付人数<50千人 | 支付人数≥50千人 | 总计 | |
微信支付 | |||
支付宝支付 | |||
总计 |
(3)根据支付人数的频率分布直方图,对两种支付方式的优劣进行比较.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个平面垂直,下列命题中错误的是( )
A.两个平面内分别垂直于交线的两条直线相互垂直
B.一个平面内的任一条直线必垂直于另一个平面.
C.一个平面内存在直线垂直于另一个平面
D.一个平面内的任意一条直线都垂直于另一个平面内的无数条直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型玩具厂研发生产一种新型玩具,年固定成本为10万元,每生产千件需另投入3万元,设该厂年内共生产该新型玩具![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且满足函数关系:
万元,且满足函数关系:![]() .
.
(1)写出年利润![]() (万元)关于该新型玩具年产量
(万元)关于该新型玩具年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在此新型玩具的生产中所获年利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com