
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求
恒成立,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若![]() 有且只有两个整数解,求
有且只有两个整数解,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
,![]() 两点.直线
两点.直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() (
(![]() ,
,![]() 与
与![]() 不重合)
不重合)
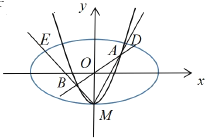
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的值;
的值;
(3)若![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速收费点处记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .比方:10点04分,记作时刻64.
.比方:10点04分,记作时刻64.
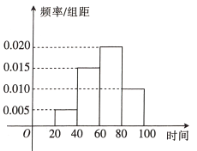
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,记![]() 为9:20~10:00之间通过的车辆数,求
为9:20~10:00之间通过的车辆数,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)由大数据分析可知,车辆在春节期间每天通过该收费点的时刻![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
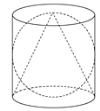
(1)试计算出图案中球与圆柱的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左焦点为
的左焦点为![]() ,过点F做x轴的垂线交椭圆于A,B两点,且
,过点F做x轴的垂线交椭圆于A,B两点,且![]() .
.
(1)求椭圆C的标准方程:
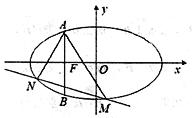
(2)若M,N为椭圆上异于点A的两点,且直线![]() 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司年初以200万元购进一艘轮船,以每年40万元的价格出租给海运公司.轮船公司负责轮船的维护,第一年维护费为4万元,随着轮船的使用与磨损,以后每年的维护费比上一年多2万元,同时该轮船第![]() 年末可以以
年末可以以![]() 万元的价格出售.
万元的价格出售.
(1)写出轮船公司到第![]() 年末所得总利润
年末所得总利润![]() 万元关于
万元关于![]() 的函数解析式,并求
的函数解析式,并求![]() 的最大值;
的最大值;
(2)为使轮船公司年平均利润最大,轮船公司应在第几年末出售轮船?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设相互垂直的直线![]() ,
,![]() 分别过椭圆
分别过椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,且与椭圆
,且与椭圆![]() 的交点分别为
的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.
(1)当![]() 的倾斜角为
的倾斜角为![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
(2)问是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com