练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为支援湖北抗击新冠疫情，无锡市某医院欲从6名医生和4名护士中抽选3人（医生和护士均至少有一人）分配到A，B，C三个地区参加医疗救援（每个地区一人），方案要求医生不能去A地区，则分配方案共有( )

    A.264种B.224种C.250种D.236种

    【答案】A

    【解析】

    分类计数，考虑选取1名医生2名护士和选取2名医生1名护士两类情况求解.

    当选取的是1名医生2名护士，共有种选法，分配到A，B，C三个地区参加医疗救援（每个地区一人），方案要求医生不能去A地区，共有种，即一共种方案；

    当选取的是2名医生1名护士，共有种选法，分配到A，B，C三个地区参加医疗救援（每个地区一人），方案要求医生不能去A地区，共有种，即一共种方案.

    综上所述：分配方案共有264种.

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下面给出三个游戏，袋子中分别装有若干只有颜色不同的小球（大小，形状，质量等均一样），从袋中无放回地取球，则其中不公平的游戏是______.

    游戏1

    游戏2

    游戏3

    球数

    3个黑球和一个白球

    一个黑球和一个白球

    2个黑球和2个白球

    取法

    取1个球，再取1个球

    取1个球

    取1个球，再取1个球

    胜利

    规则

    取出的两个球同色→甲胜

    取出的球是黑球→甲胜

    取出的两个球同色→甲胜

    取出的两个球不同色→乙胜

    取出的球是白球→乙胜

    取出的两个球不同色→乙胜

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为响应国家“节能减排，开发清洁能源”的号召，小华制作了一个太阳灶，如图所示.集光板由抛物面（抛物线绕对称轴旋转得到）形的反光镜构成，已知镜口圆的直径为，镜深，为达到最佳吸收太阳光的效果，容器灶圈应距离集光板顶点（ ）

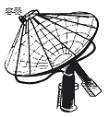
    A.0.5米B.1米C.1.5米D.2米

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数，.

    （1）若在上单调递增，求正数的最大值；

    （2）若函数在内恰有一个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

    （1）求直方图中的值；

    （2）求月平均用电量的众数和中位数；

    （3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出以下四个结论：①函数与的图象只有一个交点；②函数与的图象有无数个交点；③函数与的图象有三个交点；④函数与的图象只有一个交点.则正确结论的序号为（ ）

    A.①B.②C.③D.④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区工会利用“健步行” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分)， 每多走2千步再积20分（不足2千步不积分).为了解会员的健步走情况，工会在某天从系统中随机抽取了 1000名会员，统计了当天他们的步数，并将样本数据分为，九组，整理得到如图频率分布直方图：

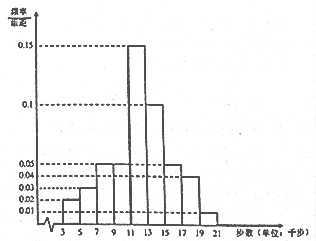
    （1）求当天这1000名会员中步数少于11千步的人数；

    （2）从当天步数在的会员中按分层抽样的方式抽取6人，再从这6人中随机抽取2人，求这2人积分之和不少于200分的概率；

    （3）写出该组数据的中位数（只写结果）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，游客从某旅游景区的景点A处下山至C处有两种路径：一种是从A处沿直线步行到C处；另一种是先从A处沿索道乘缆车到B处，然后从B处沿直线步行到C处，现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m·min-1.在甲出发2 min后，乙从A处乘缆车到B处，在B处停留1 min后，再从B处匀速步行到C处假设缆车的速度为130 m·min-1，山路AC长为1260 m，经测量，.

    （1）乙出发多长时间后，乙在缆车上与甲的距离最短？

    （2）为使甲、乙在C处互相等待的时间不超过3 min，乙步行的速度应控制在什么范围内？

    查看答案和解析>>

    同步练习册答案