练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

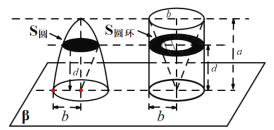
    【题目】我国南北朝时期的数学家祖暅提出了一条原理：“幂势既同，则积不容异”即夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等.椭球是椭圆绕其长轴旋转所成的旋转体，如图，将底面半径都为.高都为的半椭球和已被挖去了圆锥的圆柱（被挖去的圆锥以圆柱的上底面为底面，下底面的圆心为顶点）放置于同一平面上，用平行于平面且与平面任意距离处的平面截这两个几何体，截面分别为圆面和圆环，可以证明圆=圆环总成立.据此，椭圆的短半轴长为2，长半轴长为4的椭球的体积是（ ）

    A.B.C.D.

    【答案】C

    【解析】

    由圆=圆环总成立，求出椭球的体积，代入与的值得答案.

    解：∵圆=圆环总成立，
    ∴半椭球的体积为：，
    ∴椭球的体积，
    ∵椭球体短轴长为2，长半轴长为4，
    ∴该椭球体的体积.
    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】F是抛物线的焦点，M是抛物线C上位于第一象限内的任意一点，过三点的圆的圆心为Q，点Q到抛物线C的准线的距离为.

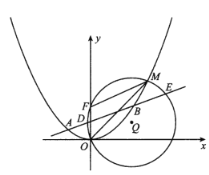
    （1）求抛物线C的方程；

    （2）若点M的横坐标为，直线与抛物线C有两个不同的交点A，B，l与圆Q有两个不同的交点D，E，求当时，的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（其中为参数，且，在以为极点、轴的非负半轴为极轴的极坐标系（两种坐标系取相同的单位长度）中，曲线的极坐标方程为，设直线经过定点，且与曲线交于、两点．

    （Ⅰ）求点的直角坐标及曲线的直角坐标方程；

    （Ⅱ）求证：不论为何值时，为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程为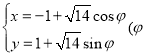为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．曲线的极坐标方程为，曲线与曲线的交线为直线．

    （1）求直线和曲线的直角坐标方程；

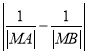    （2）直线与轴交于点，与曲线相交于，两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设V是空间中2019个点构成的集合，其中任意四点不共面某些点之间连有线段，记E为这些线段构成的集合.试求最小的正整数n，满足条件：若E至少有n个元素，则E一定含有908个二元子集，其中每个二元子集中的两条线段有公共端点，且任意两个二元子集的交为空集.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）讨论函数的单调性；

    （2）当时，证明曲线分别在点和点处的切线为不同的直线；

    （3）已知过点能作曲线的三条切线，求，所满足的条件.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】武汉出现的新型冠状病毒是一种可以通过飞沫传播的变异病毒，某药物研究所为筛查该新型冠状病毒，需要检验血液是否为阳性，现有份血液样本，每份样本取到的可能性均等，有以下两种检验方式：①逐份检验，则需要检验n次；②混合检验，将其中份血液样本分别取样混合在一起检验.若检验结果为阴性，这k份血液全为阴性，因此这k份血液样本检验一次就够了，如果检验结果为阳性，为了明确这k份血液究竟哪几份为阳性，就要对这k份血液再逐份检验，此时这k份血液的检验次数总共为次.假设在接受检验的血液样本中，每份样本的检验结果是阴性还是阳性都是独立的，且每份样本是阳性结果的概率为.

    （1）假设有5份血液样本，其中只有2份为阳性，若采取逐份检验方式，求恰好经过2次检验就能把阳性样本全部检验出来的概率；

    （2）现取其中份血液样本，记采用逐份检验方式，样本需要检验的次数为，采用混合检验方式，样本需要检验的总次数为.

    （i）试运用概率统计知识，若，试求P关于k的函数关系式；

    （ii）若，采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少，求k的最大值.

    参考数据：，，，，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年4月，河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案，决定从2018年秋季入学的高中一年级学生开始实施“”高考模式.所谓“”，即“3”是指考生必选语文、数学、外语这三科；“1”是指考生在物理、历史两科中任选一科；“2”是指考生在生物、化学、思想政治、地理四科中任选两科.

    （1）若某考生按照“”模式随机选科，求选出的六科中含有“语文，数学，外语，物理，化学”的概率.

    （2）新冠疫情期间，为积极应对“”新高考改革，某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果，从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试，并给前400名颁发荣誉证书，假设该次网络测试成绩服从正态分布，且满分为450分.

    ①考生甲得知他的成绩为270分，考试后不久了解到如下情况：“此次测试平均成绩为171分，351分以上共有57人”，请用你所学的统计知识估计甲能否获得荣誉证书，并说明理由；

    ②考生丙得知他的实际成绩为430分，而考生乙告诉考生丙：“这次测试平均成绩为201分，351分以上共有57人”，请结合统计学知识帮助丙同学辨别乙同学信息的真伪，并说明理由.

    附：；

    ；

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一个最高点为（），与之相邻的一个对称中心为，将f（x）的图象向右平移个单位长度得到函数g（x）的图象，则（ ）

    A.g（x）为偶函数

    B.g（x）的一个单调递增区间为

    C.g（x）为奇函数

    D.函数g（x）在上有两个零点

    查看答案和解析>>

    同步练习册答案