
【题目】在平面直角坐标系![]() 中,动圆
中,动圆![]() 与圆
与圆![]() 外切,与圆
外切,与圆![]() 内切.
内切.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 过点
过点![]() 且与动圆圆心
且与动圆圆心![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点.是否存在
两点.是否存在![]() 面积的最大值,若存在,求出
面积的最大值,若存在,求出![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 面积的最大值为
面积的最大值为![]() ,理由见解析.
,理由见解析.
【解析】
(1)设动圆![]() 的半径为
的半径为![]() ,利用几何关系转化两圆内切和外切的问题,可得出
,利用几何关系转化两圆内切和外切的问题,可得出![]() ,可得知点
,可得知点![]() 的轨迹是以点
的轨迹是以点![]() 、
、![]() 为焦点的椭圆,并设该椭圆的方程为
为焦点的椭圆,并设该椭圆的方程为![]() ,利用椭圆的定义求出
,利用椭圆的定义求出![]() 的值,可求出
的值,可求出![]() 的值,由此可得出动点
的值,由此可得出动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,列出韦达定理,并计算出
的方程与椭圆的方程联立,列出韦达定理,并计算出![]() 的面积关于
的面积关于![]() 的表达式,换元
的表达式,换元![]() ,利用双勾函数的单调性可得出
,利用双勾函数的单调性可得出![]() 面积的最大值.
面积的最大值.
(1)设点![]() ,动圆
,动圆![]() 的半径为
的半径为![]() ,
,
由题意知,![]() ,
,![]() ,
,![]()
由椭圆定义可知,动圆圆心![]() 在以
在以![]() 、
、![]() 为焦点的椭圆上,
为焦点的椭圆上,
设该椭圆的方程为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
由于圆![]() 内切于圆
内切于圆![]() 于点
于点![]() ,则
,则![]() .
.
因此,动圆圆心![]() 的轨迹方程为
的轨迹方程为![]() ;
;
(2)存在![]() 面积的最大值.
面积的最大值.
因为直线![]() 过点
过点![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() 或
或![]() (舍).
(舍).
则 ,整理得
,整理得 ![]() .
.
由![]() .
.
设点![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
则 ,
,
因为![]() .
.
设![]() ,则
,则![]() ,则
,则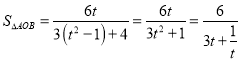 .
.
设![]() 在区间
在区间![]() 上为增函数,所以
上为增函数,所以![]() .
.
所以![]() ,当且仅当
,当且仅当![]() 时取等号,即
时取等号,即![]() .
.
因此,![]() 面积的最大值为
面积的最大值为![]() .
.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】设等差数列{an}中,a2=-8,a6=0.
(1)求数列{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.
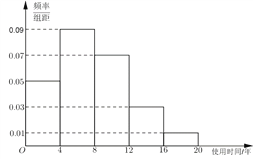

图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
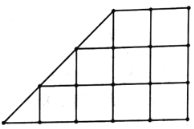
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: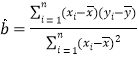 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
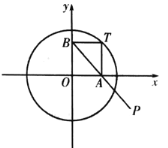
【题目】如图,点![]() 为圆
为圆![]() :
:![]() 上一动点,过点
上一动点,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() 延长至点
延长至点![]() ,使得
,使得![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,试问在曲线
两点,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线![]() 方程;若不存在,说明理由.
方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市面上有某品牌![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过5000小时,经销商对
型节能灯使用寿命都超过5000小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:

某商家因原店面需要重新装修,需租赁一家新店面进行周转,合约期一年.新店面需安装该品牌节能灯5支(同种型号)即可正常营业.经了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的两种节能灯照明效果相当,都适合安装.已知
型55瓦的两种节能灯照明效果相当,都适合安装.已知![]() 型和
型和![]() 型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
(Ⅰ)根据频率直方图估算![]() 型节能灯的平均使用寿命;
型节能灯的平均使用寿命;
(Ⅱ)根据统计知识知,若一支灯管一年内需要更换的概率为![]() ,那么
,那么![]() 支灯管估计需要更换
支灯管估计需要更换![]() 支.若该商家新店面全部安装了
支.若该商家新店面全部安装了![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(Ⅲ)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com