
【题目】曲线 ![]() 是平面内到定点
是平面内到定点 ![]() 的距离与到定直线
的距离与到定直线 ![]() 的距离之和为
的距离之和为 ![]() 的动点
的动点 ![]() 的轨迹.则曲线
的轨迹.则曲线 ![]() 与
与 ![]() 轴交点的坐标是________________;又已知点
轴交点的坐标是________________;又已知点 ![]() (
(![]() 为常数),那么
为常数),那么 ![]() 的最小值
的最小值 ![]() ________________.
________________.
科目:高中数学 来源: 题型:
【题目】某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入![]() 与时间
与时间![]() (以月为单位)的关系为
(以月为单位)的关系为![]() ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定实数 t,已知命题 p:函数![]() 有零点;命题 q: x∈[1,+∞)
有零点;命题 q: x∈[1,+∞) ![]() ≤4
≤4![]() -1.
-1.
(Ⅰ)当 t=1 时,判断命题 q 的真假;
(Ⅱ)若 p∨q 为假命题,求 t 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC﹣A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1 . 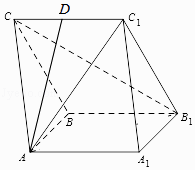
(Ⅰ)求证:平面AA1B1B⊥平面BB1C1C;
(Ⅱ)若D是CC1中点,∠ADB是二面角A﹣CC1﹣B的平面角,求直线AC1与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;③比较两个模型的拟合效果,可以比较残差平方和大小,残差平方和越小的模型拟合效果越好.其中说法正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.设p:f(x)=x3+2x2+mx+1是R上的单调增函数, ![]() ,则p是q的必要不充分条件
,则p是q的必要不充分条件
B.若命题 ![]() ,则¬p:?x∈R,x2﹣x+1>0
,则¬p:?x∈R,x2﹣x+1>0
C.奇函数f(x)定义域为R,且f(x﹣1)=﹣f(x),那么f(8)=0
D.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+ax(a∈R).
(Ⅰ)当a=0,求f(x)的最小值;
(Ⅱ)若函数g(x)=f(x)+lnx在区间[1,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)过点P(1,﹣3)恰好能作函数y=f(x)图象的两条切线,并且两切线的倾斜角互补,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com