
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (为参数,倾斜角),曲线C的参数方程为
(为参数,倾斜角),曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系。
轴正半轴为极轴建立极坐标系。
(1)写出曲线![]() 的普通方程和直线的极坐标方程;
的普通方程和直线的极坐标方程;
(2)若直线与曲线![]() 恰有一个公共点
恰有一个公共点![]() ,求点
,求点![]() 的极坐标。
的极坐标。
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币连掷三次,事件“恰出现1次反面朝上”的概率记为![]() ,现采用随机模拟的方法估计
,现采用随机模拟的方法估计![]() 的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为
的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为![]() ,则
,则![]() ,
,![]() 分别为( )
分别为( )
111 001 011 010 000 111 111 111 101 010
000 101 011 010 001 011 100 101 001 011
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
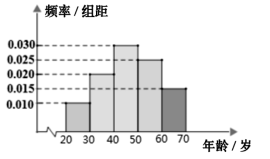
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点![]() 到两坐标轴的距离之和等于它到定点
到两坐标轴的距离之和等于它到定点![]() 的距离,记点P的轨迹为
的距离,记点P的轨迹为![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 关于原点对称;②
关于原点对称;②![]() 关于直线
关于直线![]() 对称;③直线
对称;③直线![]() 与
与![]() 有无数个公共点;④在第一象限内,
有无数个公共点;④在第一象限内,![]() 与x轴和y轴所围成的封闭图形的面积小于
与x轴和y轴所围成的封闭图形的面积小于![]() .其中正确的结论是________.(写出所有正确结论的序号)
.其中正确的结论是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com