
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若函数![]() 在
在![]() 上有零点,则一定有
上有零点,则一定有![]()
B.函数![]() 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
C.若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]()
D.若函数![]() 满足条件
满足条件![]() ,
,![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个由数字1,2,3,4,5,6,7,8,9组成的
是一个由数字1,2,3,4,5,6,7,8,9组成的![]() 位正整数,并同时满足如下两个条件:
位正整数,并同时满足如下两个条件:
(1)数字1,2,…,![]() 在
在![]() 中各出现两次;
中各出现两次;
(2)每两个相同的数字![]() 之间恰有
之间恰有![]() 个数字.
个数字.
此时,我们称这样的正整数![]() 为“好数”.例如,当
为“好数”.例如,当![]() 时,
时,![]() 可以是312 132.试确定满足条件的正整数
可以是312 132.试确定满足条件的正整数![]() 的值,并各写出一个相应的好数
的值,并各写出一个相应的好数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
甲生产线生产的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
乙生产线产生的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
|
频数 | 10 | 15 | 25 | 30 | 20 |
(1)若从乙生产线生产的产品中有放回地随机抽取3件,求至少抽到2件三等品的概率;
(2)若该产品的利润率![]() 与质量指标值
与质量指标值![]() 满足关系:
满足关系: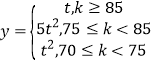 ,其中
,其中![]() ,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为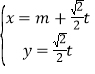 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com