
【题目】已知函数![]()
(1)当![]() 时,求
时,求![]() 的极大值;
的极大值;
(2)讨论![]() 的单调区间;
的单调区间;
(3)对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)单调递增区间是(-∞,a-2),(a,+∞),单调递减区间是(a-2,a);(3)
;(2)单调递增区间是(-∞,a-2),(a,+∞),单调递减区间是(a-2,a);(3)![]() .
.
【解析】
(1)求导,令导数为零,讨论函数的单调性,即可根据单调性求得极大值;
(2)求导,对导数分解因式,列表,写出函数的单调区间即可;
(3)对参数进行分类讨论,考虑每种情况下函数在区间上的最值,根据不等式恒成立,求得参数的取值范围.
(1)![]() 时,
时,![]()
则![]() ,
,
令![]() 解得
解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
所以![]() 时,
时,![]() 有极大值,
有极大值,
极大值为![]()
(2)f(x)=2(x-a)![]() ex+(x-a)
ex+(x-a)![]() 2ex=(x-a) [x-(a-2)]ex.
2ex=(x-a) [x-(a-2)]ex.
令f(x)=0,![]() .
.
当x变化时,f(x)、f(x)的变化如下:
x | (-∞,a-2) | a-2 | (a-2,a) | a | (a,+∞) |
f(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以f(x)的单调递增区间是(-∞,a-2),(a,+∞),单调递减区间是(a-2,a).
(3)由(2)得f(x)的极大值为f(a-2)=4ea-2.
(i)当a≤1时,
f(x)在(-∞,1]上的最大值为f(a-2)或f(1),
即可得![]() ,且
,且![]() ,
,
解得![]() ,且
,且![]() ,
,
结合![]() ,
,
解得满足题意的![]() ;
;
(ii)当![]() 即
即![]() 时,
时,
f(x)在(-∞,1]上的最大值为f(a-2)
此时f(a-2)![]() 满足题意,
满足题意,
故![]() .
.
(iii)当![]() 时,即
时,即![]() ,
,
![]() 的最大值为
的最大值为![]() ,
,
又![]() ,
,
故![]() 不恒成立
不恒成立
综上,![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且
,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且![]() 的面积是
的面积是![]() .
.
Ⅰ.求椭圆C的方程;
Ⅱ.设直线![]() 与椭圆C交于P、Q两点,点P关于x轴的对称点为
与椭圆C交于P、Q两点,点P关于x轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与x轴交于点H,求
与x轴交于点H,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布如下:
的分布如下:
|
| 7 | 8 | 9 | 10 |
| 0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率.
(Ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间上![]() ,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
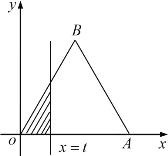
【题目】如图,在直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,直线
,直线![]()
![]() 将
将![]() 分成两部分,记左侧部分的多边形为
分成两部分,记左侧部分的多边形为![]() .设
.设![]() 各边长的平方和为
各边长的平方和为![]() ,
,![]() 各边长的倒数和为
各边长的倒数和为![]() .
.
(Ⅰ) 分别求函数![]() 和
和![]() 的解析式;
的解析式;
(Ⅱ)是否存在区间![]() ,使得函数
,使得函数![]() 和
和![]() 在该区间上均单调递减?若存在,求
在该区间上均单调递减?若存在,求![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com