
【题目】已知函数![]() .
.
(1)若![]() 的定义域,值域都是
的定义域,值域都是![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,讨论
时,讨论![]() 在区间
在区间![]() 上的值域.
上的值域.
【答案】(1)实数![]() 不存在在;(2)当
不存在在;(2)当![]() 时,值域为:
时,值域为:![]() ;
;
当![]() ,值域为
,值域为![]() ;
;
当![]() 时,值域为:
时,值域为:![]() .
.
【解析】
(1)根据对数的真数大于零,结合已知和一元二次不等式解集的性质、对数函数的单调性进行求解即可;
(2)根据复合函数的单调性,结合所给的区间,分类讨论进行求解即可.
(1)因为![]() 的定义域是
的定义域是![]() ,所以
,所以![]() 在实数集上恒成立,故一元二次方程
在实数集上恒成立,故一元二次方程![]() 的根的判别式
的根的判别式![]() ;
;
![]() 的值域是
的值域是![]() ,说明
,说明![]() 能取遍所有的正实数,因此一元二次方程
能取遍所有的正实数,因此一元二次方程![]() 的根的判别式
的根的判别式![]() ,显然这与刚得到
,显然这与刚得到![]() 矛盾,故不存在这样的实数
矛盾,故不存在这样的实数![]() ;
;
(2)因为![]() ,所以
,所以![]() ,函数的定义域为不等于1的全体实数,故区间
,函数的定义域为不等于1的全体实数,故区间![]() 的右端点不能等于1,即
的右端点不能等于1,即![]() 且
且![]() ,显然函数在
,显然函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,函数在
时,函数在![]() 上是减函数,故函数的最大值为
上是减函数,故函数的最大值为![]() ,函数的最小值为:
,函数的最小值为:![]() ,因此函数的值域为:
,因此函数的值域为:![]() ;
;
当![]() ,函数没有单调性,故函数的最大值为
,函数没有单调性,故函数的最大值为![]() ,而
,而![]() ,所以函数的值域为
,所以函数的值域为![]() ;
;
当![]() 时,函数的最大值为:
时,函数的最大值为:![]() ,而
,而![]() ,所以函数的值域为:
,所以函数的值域为:
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,x∈R.
,x∈R.
(1)若f(x)是偶函数,求实数a的值;
(2)当a>0时,不等式f(sinx![]() cosx)﹣f(4+t)≥0对任意的x∈
cosx)﹣f(4+t)≥0对任意的x∈![]() 恒成立,求实数t的取值范围;
恒成立,求实数t的取值范围;
(3)当a>0时,关于x的方程![]() 在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.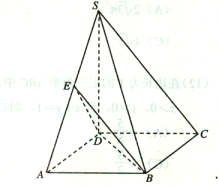
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
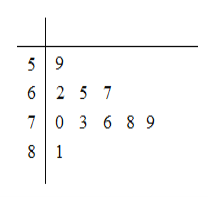
(1)若第五组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的中位数;
(3)在(2)的条件下,从体重不低于73公斤的职工中随机抽取两名职工,求被抽到的两名职工的体重之和大于或等于154公斤的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且  ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆上的四个动点,且
是椭圆上的四个动点,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 交于椭圆
交于椭圆![]() 内一点
内一点![]() .当点
.当点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的上顶点和右顶点重合时,四边形
的上顶点和右顶点重合时,四边形![]() 的面积为4.
的面积为4.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)证明:当点![]() ,
,![]() ,
,![]() ,
,![]() 在椭圆上运动时,
在椭圆上运动时,![]() (
(![]() )是定值.
)是定值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com