
【题目】已知![]() 为锐角
为锐角![]() 的外心,且三边
的外心,且三边![]() 与面积
与面积![]() 满足
满足![]() ,若
,若![]() (其中
(其中![]() 是实数),则
是实数),则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
利用余弦定理以及三角形的面积公式求出![]() ,以
,以![]() 边所在的直线为
边所在的直线为![]() 轴,
轴,![]() 边的垂直平分线为
边的垂直平分线为![]() 轴建立直角坐标系(
轴建立直角坐标系(![]() 为
为![]() 边的中点),由外接圆的性质可得
边的中点),由外接圆的性质可得![]() ,由
,由![]() ,不妨设外接圆的半径
,不妨设外接圆的半径![]() ,则
,则![]() ,可得
,可得![]() 的坐标,设
的坐标,设![]() ,则
,则![]() 的外接圆的方程为:
的外接圆的方程为:![]() ,利用向量的坐标运算可得
,利用向量的坐标运算可得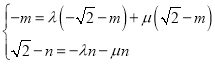 ,从而求出
,从而求出![]() ,代入外接圆方程可得
,代入外接圆方程可得![]() ,再利用基本不等式即可求解.
,再利用基本不等式即可求解.
由![]() ,可知
,可知![]() ,
,
解得![]() ,所以
,所以![]() ,
,
如图所示,以![]() 边所在的直线为
边所在的直线为![]() 轴,
轴,![]() 边的垂直平分线为
边的垂直平分线为![]() 轴建立直角坐标系
轴建立直角坐标系
(![]() 为
为![]() 边的中点)
边的中点)
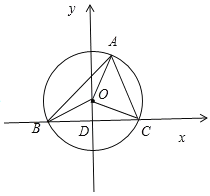
由外接圆的性质可得![]() ,
,
由![]() ,不妨设外接圆的半径
,不妨设外接圆的半径![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则![]() 的外接圆的方程为:
的外接圆的方程为:![]() ,
,
![]() ,
,
![]() ,
,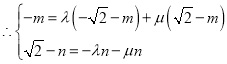 ,
,
![]() ,否则
,否则![]() 三点共线,由图可知不可能的.
三点共线,由图可知不可能的.
![]() 可化为
可化为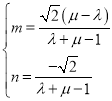 ,代入
,代入![]() 的外接圆的方程可得
的外接圆的方程可得
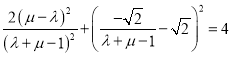 ,
,
化为![]() ,
,
化为![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.
故选:D


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
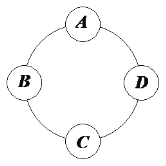
【题目】为配合“2019双十二”促销活动,某公司的四个商品派送点如图环形分布,并且公司给![]() 四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给
四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给![]() 四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
A.最少需要16次调动,有2种可行方案
B.最少需要15次调动,有1种可行方案
C.最少需要16次调动,有1种可行方案
D.最少需要15次调动,有2种可行方案
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,楔形几何体![]() 由一个三棱柱截去部分后所得,底面
由一个三棱柱截去部分后所得,底面![]() 侧面
侧面![]() ,
,![]() ,楔面
,楔面![]() 是边长为2的正三角形,点
是边长为2的正三角形,点![]() 在侧面
在侧面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,点
,点![]() 在
在![]() 上,且
上,且![]()

(1)证明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 与侧面
与侧面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校某年级学生的阅读量(分钟),随机抽取了n名学生,调查他们一天的阅读时间,统计结果下图表所示:
组号 | 分组 | 男生 人数 | 男生人数占本 组人数的频率 | 频率分布直方图 |
第1组 |
| 5 | 0.5 |
|
第2组 |
| 18 | 0.9 | |
第3组 |
| 24 | 0.8 | |
第4组 |
|
| 0.4 | |
第5组 |
| 3 | 0.2 |
(1)求出![]() 与
与![]() 的值;
的值;
(2)—天的阅时间不少于35分钟称为“喜好阅读者”.根据以上数据,完成下面的![]() 列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
喜好阅读者 | 非喜好阅读者 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: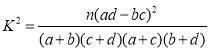 (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com