
【题目】已知函数f(x)=![]() +
+![]() .
.
(1)当m=0时,求不等式f(x)≤9的解集;
(2)当m=2时,若x∈(1,4),f(x) ![]() 2x
2x![]() a<0,求a的取值范围.
a<0,求a的取值范围.
【答案】(1) {x|![]()
![]() ≤x≤
≤x≤![]() }. (2) a∈[3,+∞).
}. (2) a∈[3,+∞).
【解析】
(1) 对![]() 分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果;(2)原不等式等价于
分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果;(2)原不等式等价于![]() x+2
x+2![]() a<2x
a<2x![]() 4<x
4<x![]() 2+a,得
2+a,得![]() <x<a+2,可得(1,4)(
<x<a+2,可得(1,4)(![]() ,a+2), 根据包含关系列不等式求解即可.
,a+2), 根据包含关系列不等式求解即可.
(1)f(x)=|2x![]() 4|+|x|≤9,
4|+|x|≤9,
即![]() 或
或![]() 或
或![]()
得2<x≤![]() 或0≤x≤2或
或0≤x≤2或![]()
![]() ≤x<0.
≤x<0.
所以f(x)≤9的解集为{x|![]()
![]() ≤x≤
≤x≤![]() }.
}.
(2)当m=2时,f(x) ![]() 2x
2x![]() a<0对x∈(1,4)恒成立,
a<0对x∈(1,4)恒成立,
等价于![]() <x
<x![]() 2+a,x∈(1,4)恒成立.
2+a,x∈(1,4)恒成立.
由![]() x+2
x+2![]() a<2x
a<2x![]() 4<x
4<x![]() 2+a,得
2+a,得![]() <x<a+2,
<x<a+2,
由题意得(1,4)(![]() ,a+2),
,a+2),
所以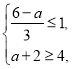 解得a≥3,即a∈[3,+∞).
解得a≥3,即a∈[3,+∞).


科目:高中数学 来源: 题型:
【题目】2017年10月18日至10月24日,中国共产党第十九次全国代表大会![]() 简称党的“十九大”
简称党的“十九大”![]() 在北京召开
在北京召开![]() 一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在
一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在![]() 内,按成绩分成5组:第1组
内,按成绩分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
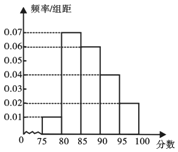
![]() 求这100人的平均得分
求这100人的平均得分![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 求第3,4,5组分别选取的作深入学习的人数;
求第3,4,5组分别选取的作深入学习的人数;
![]() 若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求cosC;
(2)若c![]() ,△ABC的面积为
,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与两个定点
与两个定点![]() 距离的比是一个正数
距离的比是一个正数![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)当![]() 时得曲线
时得曲线![]() 的方程,把曲线
的方程,把曲线![]() 向左平移三个单位长度得到曲线
向左平移三个单位长度得到曲线![]() ,已知点
,已知点![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值;
的最小值;
(3)若直线![]() 与曲线
与曲线![]() 交于C、D两点,点
交于C、D两点,点![]() 是x轴上的点,使得
是x轴上的点,使得![]() 恒为定值,求点P的坐标和定值.
恒为定值,求点P的坐标和定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构用“10分制”调查了各阶层人士对某次国际马拉松赛事的满意度,现从调查人群中随机抽取16名,如图茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若满意度不低于9.5分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() 1,双曲线的一支上不同的三点A(x1,y1),B(6,
1,双曲线的一支上不同的三点A(x1,y1),B(6,![]() ),C(x2,y2)到焦点F(5,0)的距离成等差数列.
),C(x2,y2)到焦点F(5,0)的距离成等差数列.
(1)求m的值;
(2)试求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com