
【题目】已知函数![]() ,其导函数为
,其导函数为![]() ,函数
,函数![]() ,对任意
,对任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求实数![]() 的值;
的值;
(2)若![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知![]() ,将
,将![]() 的图像向右平移
的图像向右平移![]() 个单位后,再保持纵坐标不变,横坐标变为原来的2倍,得到函数
个单位后,再保持纵坐标不变,横坐标变为原来的2倍,得到函数![]() 的图象.
的图象.
(1)求函数![]() 在
在![]() 上的值域及单调递增区间;
上的值域及单调递增区间;
(2)若![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为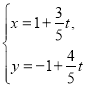 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
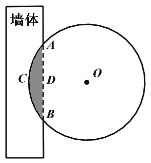
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).己知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,
寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,![]() )
)
A.300立方寸B.305.6立方寸C.310立方寸D.316.6立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,记以
两点,记以![]() ,
,![]() 为直径端点的圆为圆
为直径端点的圆为圆![]() .
.
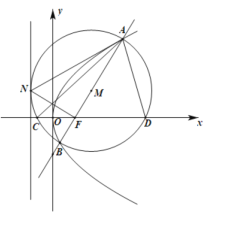
(1)证明:圆![]() 与抛物线的准线相切;
与抛物线的准线相切;
(2)设![]() ,点
,点![]() 在焦点的右侧,圆
在焦点的右侧,圆![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,记
两点,记![]() 和
和![]() 的面积为
的面积为![]() ,
,![]() 求
求![]() 的最大值(其中,点
的最大值(其中,点![]() 为圆
为圆![]() 与抛物线准线的切点)
与抛物线准线的切点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com