
【题目】已知椭圆![]()
![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,
, ![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的面积为
的面积为![]() ,且该四边形内切圆的方程为
,且该四边形内切圆的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个不同的动点,直线
上的两个不同的动点,直线![]() 、
、![]() 的斜率之积等于
的斜率之积等于![]() ,试探求
,试探求![]() 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(1)利用题意求得![]() ,
, ![]() ,则椭圆
,则椭圆![]() 的方程为:
的方程为: ![]() ;
;
(2)分别考查斜率存在和斜率不存在两种情况,求得![]() 的面积为定值
的面积为定值![]() .
.
试题解析:
(Ⅰ)![]() 四边形
四边形![]() 的面积为
的面积为![]() ,又可知四边形
,又可知四边形![]() 为菱形,
为菱形,
![]() ,即
,即![]() ①
①
由题意可得直线![]() 方程为:
方程为: ![]() ,即
,即![]()
![]() 四边形
四边形![]() 内切圆方程为
内切圆方程为![]()
![]() 圆心
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即![]() ②
②
由①②解得: ![]() ,
, ![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为: ![]()
(Ⅱ)若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
由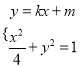 得:
得: ![]()
![]() 直线
直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两个不同的点,
两个不同的点,
![]()
![]() 得:
得: ![]() ③
③
由韦达定理: ![]()
![]() 直线
直线![]() 的斜率之积等于
的斜率之积等于![]() ,
,
![]()
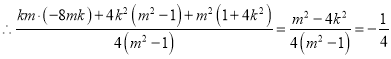
![]() 满足③
满足③
![]()
又![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
![]()
所以![]() 的面积
的面积
![]()
若直线![]() 的斜率不存在,
的斜率不存在, ![]() 关于
关于![]() 轴对称
轴对称
设![]() ,
, ![]() ,则
,则![]() ,
, ![]()
又![]()
![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]()
所以![]() 的面积
的面积
![]()
综上可知, ![]() 的面积为定值
的面积为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sin2x+2+2cos2x.
sin2x+2+2cos2x.
(1)求f(x)的最小正周期与单调递减区间;
(2)在△ABC中,a,b,c分别是角A、B、C的对边,若f(A)=4,b=1,△ABC的面积为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是 ![]() ,则sin2θ﹣cos2θ的值等于( )
,则sin2θ﹣cos2θ的值等于( ) 
A.1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(
=( ![]() sinx,m+cosx),
sinx,m+cosx), ![]() =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= ![]()
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com