
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
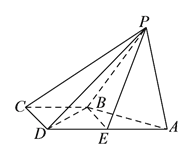
(![]() )求证:
)求证:![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在平面
)在平面![]() 内是否存在
内是否存在![]() ,使得直线
,使得直线![]() 平面
平面![]() ,请说明理由.
,请说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:
(1)由平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,故证得
,故证得![]() .(2)先证明四边形
.(2)先证明四边形![]() 是正方形,连结
是正方形,连结![]() ,则
,则![]() .又可证得四边形
.又可证得四边形![]() 是平行四边形,故
是平行四边形,故![]() ,可得
,可得![]() .根据(1)得
.根据(1)得![]() 平面
平面![]() ,故
,故![]() ,从而可得
,从而可得![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .(3)当
.(3)当![]() 为直线
为直线![]() 的交点时,满足
的交点时,满足![]() 平面
平面![]() ,根据线面平行的判定定理可证明.
,根据线面平行的判定定理可证明.
试题解析:
(![]() )证明:∵平面
)证明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() .
.
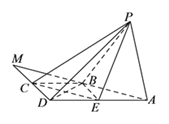
(![]() )由已知,
)由已知,![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,![]() ,
,
∴四边形![]() 是正方形,
是正方形,
连结![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
由(![]() )知
)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(3)当![]() 为直线
为直线![]() 的交点时,有
的交点时,有![]() 平面
平面![]() .
.
理由如下:
在四边形![]() 中,
中,![]() ,
,![]() ,
,
∴四边形![]() 为梯形,
为梯形,
∴![]() 必定相交,设交点为
必定相交,设交点为![]() .
.
由(2)知四边形![]() 是正方形,
是正方形,
∴![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
故平面![]() 内存在
内存在![]() ,使得直线
,使得直线![]() 平面
平面![]() ,且
,且![]() 为直线
为直线![]() 的交点.
的交点.


科目:高中数学 来源: 题型:
【题目】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
(1)求数列{an}的通项公式;
(2){bn}为各项非零的等差数列,其前n项和为Sn.已知S2n+1=bnbn+1,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是增函数.
是增函数.
(1)若命题![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题
为假命题![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(m, ![]() )(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
)(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
(1)当m=2时,求圆A的标准方程;
(2)当m变化时,△OBC的面积是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)设直线![]() 与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() .
. ![]() 表示
表示![]() 中所有不同值的个数.
中所有不同值的个数.
(![]() )设集合
)设集合![]() ,
, ![]() ,分别求
,分别求![]() 和
和![]() .
.
(![]() )若集合
)若集合![]() ,求证:
,求证: ![]() .
.
(![]() )
)![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+b,x∈[-1,1],a,b∈R,且是常数.
(1)若a是从-2,-1,0,1,2五个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求函数y=f(x)为奇函数的概率;
(2)若a是从区间[-2,2]中任取的一个数,b是从区间[0,2]中任取的一个数,求函数y=f(x)有零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光对物体的照度与光的强度成正比,比例系数为![]() ,与光源距离的平方成反比,比例系数为
,与光源距离的平方成反比,比例系数为![]() 均为正常数
均为正常数![]() 如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上
如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上![]() 不含A,
不含A,![]() 若物体P到光源A的距离为x.
若物体P到光源A的距离为x.
![]()
![]() 试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
![]() 当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com