
【题目】![]() ,
,![]() ,…,
,…,![]() 是一个数列,对每个
是一个数列,对每个![]() ,
,![]() ,
,![]() .如果
.如果![]() ,
,![]() 两数不同,写
两数不同,写![]() ;如果
;如果![]() ,
,![]() 两数相同,写
两数相同,写![]() .于是得到一个新数列
.于是得到一个新数列![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() .重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
.重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
【答案】见解析
【解析】
用![]() 表示所求数目的最大值,当
表示所求数目的最大值,当![]() 时,
时,![]() ;对于
;对于![]() ,
,![]() ;对于
;对于![]() ,
,![]() ;因为
;因为![]() ,
,![]() ,
,![]() 一共有6种可能的排列;0,0,0;1,1,1;1,0,1;1,1,0;0,1,1;0,1,0;在第2,3,4种情况时,
一共有6种可能的排列;0,0,0;1,1,1;1,0,1;1,1,0;0,1,1;0,1,0;在第2,3,4种情况时,![]() ,其余情况皆小于4.
,其余情况皆小于4.
现在寻找![]() 与
与![]() 的关系,考虑
的关系,考虑![]() 行情况,前三行为
行情况,前三行为
![]()
![]()
![]() …
… ![]()
![]()
![]()
![]()
![]()
![]()
![]() …
… ![]()
![]()
![]()
![]()
![]() …
… ![]()
![]()
下面证明,在前三行中,有不少于![]() 个零,如果
个零,如果![]() 三数中至少有一个零,将这三数作为一组,捆在一起,放入一个盒内,如果某
三数中至少有一个零,将这三数作为一组,捆在一起,放入一个盒内,如果某![]() 全为1,那么,
全为1,那么,![]() ,
,![]() ,
,![]() 及
及![]() 两组,捆在一起,至少有两个零,也放入这个盒内,那么从第一组
两组,捆在一起,至少有两个零,也放入这个盒内,那么从第一组![]() 开始,依次进行上述操作,最后,有两种可能:第一种可能
开始,依次进行上述操作,最后,有两种可能:第一种可能![]() 已放入盒内,这时盒内至少有
已放入盒内,这时盒内至少有![]() 个零,最后三数
个零,最后三数![]() 至少有一个零;第二种可能
至少有一个零;第二种可能![]() 由于全为1,没放入盒内,这时盒内至少有
由于全为1,没放入盒内,这时盒内至少有![]() 个零,但
个零,但![]() ,
,![]() ,两组
,两组![]() 与
与![]() 中至少有两个零,因此,前三行至少有
中至少有两个零,因此,前三行至少有![]() 个零,换句话讲,前三行至多
个零,换句话讲,前三行至多![]() 个1,那么有
个1,那么有![]() . ①
. ①
当![]() 时,从上式,有
时,从上式,有
![]() ,
,
![]() ,
,
![]() ,
,
……
![]()
![]() .
.
上述不等式相加,有![]() . ②
. ②
当![]() ,从①出发,类似可证
,从①出发,类似可证![]() . ③
. ③
当![]() ,有
,有![]() . ④
. ④
②、③和④可以合并为一个不等式![]() . ⑤
. ⑤
![]() 能达到,看下图.
能达到,看下图.
1 1 0 1 1 0 1 1 0
0 1 1 0 1 1 0 1
1 0 1 1 0 1 1
1 1 0 1 1 0
0 1 1 0 1
1 0 1 1
1 1 0
0 1
1
每三行作为一段,在一段内,第一行是1,1,0三数不断周期出现,第一行数的个数恰为3的倍数.第二行是0,1,1三数不断周期出现,最后二个数字是0,1,第三行是1,0,1三数不断周期出现,最后一个数字是1,换句话讲,倒过来数,每行1的数目分别为1,1,2,3,3,4,5,5,6,…,那么,
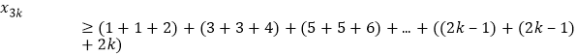
![]() , ⑥
, ⑥
![]()
![]() , ⑦
, ⑦
![]() , ⑧
, ⑧
这里![]() 是正整数.当
是正整数.当![]() 时,⑦、⑧也是正确的.
时,⑦、⑧也是正确的.
由⑥、⑦和⑧可以合并为一个不等式![]() .
.
因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且当
,且当![]() ,
,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式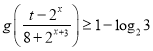 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.

(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象相邻两条对称轴之间的距离为
图象相邻两条对称轴之间的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到的图象关于
个单位,得到的图象关于![]() 轴对称,则( )
轴对称,则( )
A. 函数![]() 的周期为
的周期为![]() B. 函数
B. 函数![]() 图象关于点
图象关于点![]() 对称
对称
C. 函数![]() 图象关于直线
图象关于直线![]() 对称 D. 函数
对称 D. 函数![]() 在
在![]() 上单调
上单调
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 面
面![]() ;
;
(Ⅱ)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(3)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成的角最小时,求线段
所成的角最小时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴的正半轴于
轴的正半轴于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 方程为
方程为![]() (
(![]() ),且
),且![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 经过点
经过点![]() ,设
,设![]() 的斜率为
的斜率为![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com