练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    曲线2y2+3x+3=0与曲线x2+y2-4x-5=0的公共点的个数是（ ）
    A．4
    B．3
    C．2
    D．1
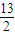
    【答案】分析：将两个曲线方程联解，消去y得得2x2-11x-13=0，解之得x=-1或x=．再将x的回代到方程中，解之可得只有x=-1、y=0符合题意．由此即可得到两个曲线有唯一的公共点，得到答案．
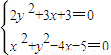
    解答：解：由消去y2，得2x2-11x-13=0
    解之得x=-1或x=
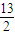
    当x=-1，代入第一个方程，得y=0；
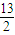
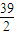
    当x=时，代入第一个方程得2y2++3=0，没有实数解
    因此，两个曲线有唯一的公共点（-1，0）
    故选：D
    点评：本题求两个已知曲线公共点的个数，着重考查了曲线与方程、二元方程组的解法等知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1991•云南）曲线2y2+3x+3=0与曲线x2+y2-4x-5=0的公共点的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    曲线2y2+3x+3=0与曲线x2+y2－4x－5=0的公共点的个数是 (　　  )

    A.4　　　　　　 B.3　　　　　　 C.2　　　　    D.1

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    曲线2y2+3x+3=0与曲线x2+y2－4x－5=0的公共点的个数是 (　　  )

    A.4　　　　　　 B.3　　　　　　 C.2　　　　    D.1

    查看答案和解析>>

    科目：高中数学 来源：云南 题型：单选题

    曲线2y2+3x+3=0与曲线x2+y2-4x-5=0的公共点的个数是（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    同步练习册答案