
(13分)已知函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)讨论函数 的单调性.
的单调性.
(1)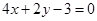 .
.
(2)当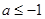 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;当
单调递增;当 时,
时,  在
在 和
和 单调递增,在
单调递增,在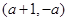 单调递减;当
单调递减;当 时,
时, 在
在 单调递增;当
单调递增;当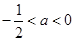 时,
时, 在
在 和
和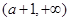 单调递增,在
单调递增,在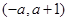 单调递减;当
单调递减;当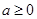 时,
时, 在
在 单调递减,在
单调递减,在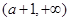 单调递增。
单调递增。
解析试题分析:(1)通过求导数,确定得到切线的斜率,利用直线方程的点斜式,即得解.
(2)求导数,求驻点,得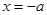 或
或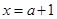 .分以下情况讨论.
.分以下情况讨论.
1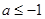 ;2
;2 ;3
;3 ;4
;4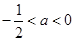 ; 5
; 5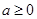 等,明确函数
等,明确函数 的单调区间.
的单调区间.
试题解析:(1) 时,
时,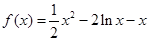 ,
, ,
, ,
,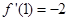 ,所以所求切线方程为
,所以所求切线方程为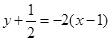 ,即
,即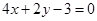 .
.
(2)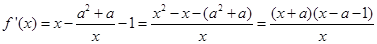 ,令
,令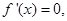 得
得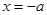 或
或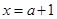 .
.
1当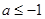 时,
时, ,所以
,所以 在
在 单调递减,在
单调递减,在 单调递增;
单调递增;
2当 时,
时,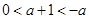 ,所以
,所以 在
在 和
和 单调递增,在
单调递增,在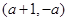 单调递减;
单调递减;
3当 时,
时, ,所以
,所以 在
在 单调递增;
单调递增;
4当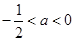 时,
时, ,所以
,所以 在
在 和
和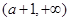 单调递增,在
单调递增,在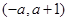 单调递减;
单调递减;
5当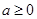 时,
时, ,所以
,所以 在
在 单调递减,在
单调递减,在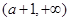 单调递增。
单调递增。
综上,当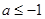 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;当
单调递增;当 时,
时,  在
在 和
和 单调递增,在
单调递增,在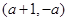 单调递减;当
单调递减;当 时,
时, 在
在 单调递增;当
单调递增;当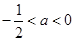 时,
时, 在
在 和
和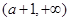 单调递增,在
单调递增,在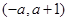 单调递减;当
单调递减;当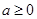 时,
时, 在
在 单调递减,在
单调递减,在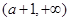 单调递增。
单调递增。
考点:导数的几何意义,应用导数研究函数的单调性.


科目:高中数学 来源: 题型:解答题
已知函数 (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数).
(Ⅰ)若 ,试判断函数
,试判断函数 在区间
在区间 上的单调性;
上的单调性;
(Ⅱ)若 ,当
,当 时,试比较
时,试比较 与2的大小;
与2的大小;
(Ⅲ)若函数 有两个极值点
有两个极值点 ,
, (
( ),求k的取值范围,并证明
),求k的取值范围,并证明 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 =
= 。
。
(1)当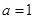 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)求函数 在区间
在区间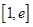 上的最小值;
上的最小值;
(3)在(1)的条件下,设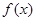 =
= +
+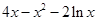 ,
,
求证: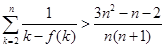 (
(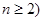 ),参考数据:
),参考数据: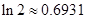 。(13分)
。(13分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).
(I)将S表示为 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com