
【题目】已知![]() ,
,![]() 实数,函数
实数,函数![]() ,函数
,函数![]() .
.
(Ⅰ)令![]() ,当
,当![]() 时,试讨论函数
时,试讨论函数![]() 在其定义域内的单调性;
在其定义域内的单调性;
(Ⅱ)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
【答案】(Ⅰ)见详解;(Ⅱ)![]()
【解析】分析:(Ⅰ)求导,讨论参数![]() 的大小,进而研究函数的定义域和导数的符号变化,再确定函数的单调性;(Ⅱ)构造函数,讨论
的大小,进而研究函数的定义域和导数的符号变化,再确定函数的单调性;(Ⅱ)构造函数,讨论![]() 的范围和
的范围和![]() 的大小关系,将问题转化为求函数的最值问题,再利用导数的符号变化确定函数的单调性,进而确定函数的最值.
的大小关系,将问题转化为求函数的最值问题,再利用导数的符号变化确定函数的单调性,进而确定函数的最值.
详解:(Ⅰ) ![]()
1. ![]() ,此时函数的定义域为
,此时函数的定义域为![]() ,
,![]() 故函数
故函数![]() 在
在![]() 内单调递增, 在
内单调递增, 在![]() 内单调递减.
内单调递减.
2. ![]() ,
,![]() ,
,
此时函数![]() 的定义域为
的定义域为![]() ,
,
令![]() ,此时
,此时![]() 恒成立. 令
恒成立. 令![]() 得,
得,![]()
函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减.
内单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减;当
内单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增, 在
内单调递增, 在![]() 内单调递减.
内单调递减.
(Ⅱ)当![]() 时,假设存在实数
时,假设存在实数![]() 满足条件,
满足条件,
则![]() 在
在![]() 上恒成立.
上恒成立.
1. 当![]() 时,
时,![]()
可化为![]() ,
,
令![]()
问题转化为:![]() 对任意
对任意![]() 恒成立(*);
恒成立(*);
又![]()
![]()
![]()
(1)![]() 时,因为
时,因为![]() ,
,
故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递减,
时单调递减,![]() ,
,
即![]() ,从而函数
,从而函数![]() 在
在![]() 时单调递增,
时单调递增,
故![]() ,所以(*)成立,满足题意;
,所以(*)成立,满足题意;
(2) 当![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,记
,记![]() ,则当
,则当![]() 时,
时,![]() ,
,
故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,
从而函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(*)不成立;
,此时(*)不成立;
所以当![]() ,
,![]() 恒成立时,
恒成立时,![]() ;
;
2. 当![]() 时,
时,![]()
可化为![]()
令![]() ,
,
问题转化为:![]() 对任意的
对任意的![]() 恒成立(**);
恒成立(**);
又![]()
![]()
![]()
(1)![]() 时,
时,![]() ,故
,故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递增,
时单调递增,![]() ,即
,即![]() ,
,
从而函数![]() 在
在![]() 时单调递增,所以
时单调递增,所以![]() ,此时(**)成立;
,此时(**)成立;
(2) 当![]() 时,
时,
①若![]() ,必有
,必有![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() ,
,
从而函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(**)不成立;
,此时(**)不成立;
② 若![]() ,则
,则![]() ,所以
,所以![]() 时,
时,![]()
故函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(**)不成立;
,此时(**)不成立;
所以当![]() ,
,![]() 恒成立时,
恒成立时,![]() .
.
综上所述,当![]() ,
,![]() 恒成立时,
恒成立时,![]() ,
,
从而实数![]() 的取值集合为
的取值集合为![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了![]() 三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列
三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,试根据下列条件求出三款软件的激活码
,以此类推,试根据下列条件求出三款软件的激活码
(1)A款应用软件的激活码是该数列中第四个三位数的项数的平方
(2)B款应用软件的激活码是该数列中第一个四位数及其前所有项的和
(3)C款应用软件的激活码是满足如下条件的最小整数![]() :①
:①![]() ;②该数列的前
;②该数列的前![]() 项和为2的整数幂
项和为2的整数幂
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
.某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
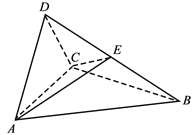
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
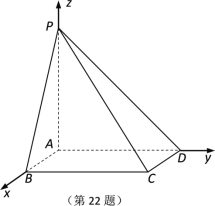
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以椭圆![]() 的离心率为
的离心率为![]() ,以其四个顶点为顶点的四边形的面积等于
,以其四个顶点为顶点的四边形的面积等于![]() .
.
![]() 1
1![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 2
2![]() 过原点且斜率不为0的直线
过原点且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 是椭圆
是椭圆![]() 的右顶点,直线
的右顶点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,问:以
,问:以![]() 为直径的圆是否恒过
为直径的圆是否恒过![]() 轴上的定点?若恒过
轴上的定点?若恒过![]() 轴上的定点,请求出该定点的坐标;若不恒过
轴上的定点,请求出该定点的坐标;若不恒过![]() 轴上的定点,请说明理由.
轴上的定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
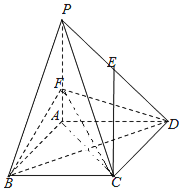
【题目】在四棱锥![]() 中,底面ABCD是边长为6的菱形,且
中,底面ABCD是边长为6的菱形,且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,F是棱PA上的一个动点,E为PD的中点.
,F是棱PA上的一个动点,E为PD的中点.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() .
.
![]() Ⅱ
Ⅱ![]() 若
若![]() .
.
![]() 求PC与平面BDF所成角的正弦值;
求PC与平面BDF所成角的正弦值;
![]() 侧面PAD内是否存在过点E的一条直线,使得该直线上任一点M与C的连线,都满足
侧面PAD内是否存在过点E的一条直线,使得该直线上任一点M与C的连线,都满足![]() 平面BDF,若存在,求出此直线被直线PA、PD所截线段的长度,若不存在,请明理由.
平面BDF,若存在,求出此直线被直线PA、PD所截线段的长度,若不存在,请明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
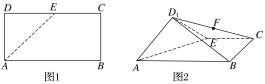
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线C的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com