
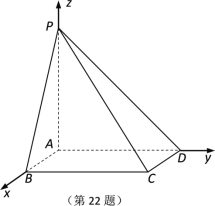
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
【答案】(1)![]() ;(2)M为AB的中点,N为PC的中点
;(2)M为AB的中点,N为PC的中点
【解析】
(1)由题意知,AB,AD,AP两两垂直.以![]() 为正交基底,建立空间直角坐标系
为正交基底,建立空间直角坐标系![]() ,求平面PCD的一个法向量为
,求平面PCD的一个法向量为![]() ,由空间向量的线面角公式求解即可;(2)设
,由空间向量的线面角公式求解即可;(2)设![]()
![]() ,利用
,利用![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() ,得到
,得到![]() 的方程,求解即可确定M,N的位置
的方程,求解即可确定M,N的位置
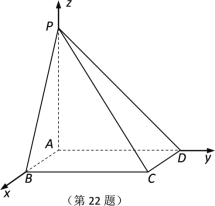
(1)由题意知,AB,AD,AP两两垂直.
以![]() 为正交基底,建立如图所示的空间
为正交基底,建立如图所示的空间
直角坐标系![]() ,则
,则![]()
从而![]()
设平面PCD的法向量![]()
则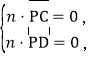 即
即![]()
不妨取![]() 则
则![]() .
.
所以平面PCD的一个法向量为![]() .
.
设直线PB与平面PCD所成角为![]() 所以
所以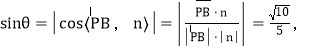
即直线PB与平面PCD所成角的正弦值为![]() .
.
(2)设![]() 则
则![]()
设![]() 则
则![]() 而
而![]()
所以![]() .由(1)知,平面PCD的一个法向量为
.由(1)知,平面PCD的一个法向量为![]() ,因为
,因为![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() .
.
所以![]() 解得,
解得,![]() .
.
所以M为AB的中点,N为PC的中点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战和不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下![]() 列联表:
列联表:
性别 成绩 | 接受挑战 | 不接受挑战 | 总计 |
男性 | 45 | 15 | 60 |
女性 | 25 | 15 | 40 |
总计 | 70 | 30 | 100 |
根据表中数据,能有有90%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:![]() ,其中
,其中![]() .
.
| 2.706 | 3.841 | 6.635 | 10.828 |
| 0.10 | 0.05 | 0.010 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且圆心C在直线x+y-1=0上.
(1)求圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)对称轴为![]() ,最小正周期
,最小正周期![]() ;(2)
;(2)![]()
【解析】
(1)利用正余弦的二倍角公式和辅助角公式将函数解析式进行化简得到![]() ,由周期公式和对称轴公式可得答案;(2)由x的范围得到
,由周期公式和对称轴公式可得答案;(2)由x的范围得到![]() ,由正弦函数的性质即可得到值域.
,由正弦函数的性质即可得到值域.
(1)![]()
![]()
令![]() ,则
,则
![]() 的对称轴为
的对称轴为![]() ,最小正周期
,最小正周期![]() ;
;
(2)当![]() 时,
时,![]() ,
,
因为![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
在![]() 取最大值,在
取最大值,在![]() 取最小值,
取最小值,
所以![]() ,
,
所以![]() .
.
【点睛】
本题考查正弦函数图像的性质,考查周期性,对称性,函数值域的求法,考查二倍角公式以及辅助角公式的应用,属于基础题.
【题型】解答题
【结束】
21
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com