
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)求导,分![]() 、
、![]() 及
及![]() 三种情况讨论即可;
三种情况讨论即可;
(2)易知函数![]() 与函数
与函数![]() 的单调性一致,然后分类讨论验证即可.
的单调性一致,然后分类讨论验证即可.
解:(1)由![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() 得,
得,![]() ,此时函数
,此时函数![]() 单调递减;令
单调递减;令![]() 得,
得,![]() ,此时函数
,此时函数![]() 单调递增;
单调递增;
当![]() 时,令
时,令![]() 得,
得,![]() ,此时函数
,此时函数![]() 单调递减;令
单调递减;令![]() 得,
得,![]() ,此时函数
,此时函数![]() 单调递增;
单调递增;
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)设![]() ,则
,则![]() 的单调性与
的单调性与![]() 的单调性一致,
的单调性一致,
当![]() 时,
时,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时, ![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,满足题意;
,满足题意;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,不合题意;
,不合题意;
综上,实数![]() 的取值范围为
的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】棉花的纤维长度是棉花质量的重要指标.在一批棉花中抽测了60根棉花的纤维长度(单位:![]() ),将样本数据制作成如下的频率分布直方图:
),将样本数据制作成如下的频率分布直方图:
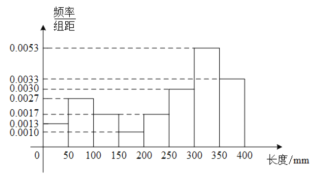
下列关于这批棉花质量状况的分析不正确的是( )
A.纤维长度在![]() 的棉花的数量为9根
的棉花的数量为9根
B.从这60根棉花中随机选取1根,其纤维长度在![]() 的概率为0.335
的概率为0.335
C.有超过一半的棉花纤维长度能达到![]() 以上
以上
D.这批棉花的纤维长度的中位数的估计值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,短轴长为2,过定点
,短轴长为2,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间).
之间).
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是曲线
是曲线![]() :
:![]() (
(![]() 为参数)上的动点,以坐标原点
为参数)上的动点,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,以极点
轴的正半轴为极轴建立极坐标系,以极点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() 的坐标为
的坐标为![]() ,射线
,射线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对于任意
满足:对于任意![]() ,
,![]() 均为数列
均为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() ,试判断数列
,试判断数列![]() 是否为“
是否为“![]() 数列”?说明理由;
数列”?说明理由;
(2)若公差为![]() 的等差数列
的等差数列![]() 为“
为“![]() 数列”,求
数列”,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 为“
为“![]() 数列”,
数列”,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2020年春,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播,我国科研人员,在研究新型冠状病毒某种疫苗的过程中,利用小白鼠进行科学试验.为了研究小白鼠连续接种疫苗后出现![]() 症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为
症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若某只小白鼠出现![]() 症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
(2)若某只小白鼠在一个接种周期内出现2次或3次![]() 症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为
症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
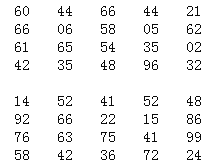
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设![]() ,五个正方形的面积和为
,五个正方形的面积和为![]() .
.
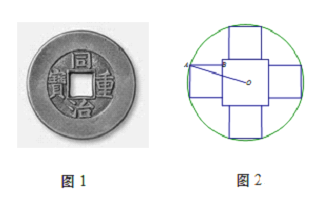
(1)求面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的范围;
的范围;
(2)求面积![]() 最小值.
最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com