
【题目】已知函数![]()
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)对函数![]() 求导,讨论当
求导,讨论当![]() 时,
时,![]() 时,
时,![]() 时,
时,![]() 时,由导数大于0,可得增区间,由导数小于0,可得减区间;(Ⅱ)由(Ⅰ)的单调区间,对
时,由导数大于0,可得增区间,由导数小于0,可得减区间;(Ⅱ)由(Ⅰ)的单调区间,对![]() 讨论,结合单调性和函数值的变化特点,即可得到所求范围.
讨论,结合单调性和函数值的变化特点,即可得到所求范围.
(Ⅰ)由题![]() ,
,
(1)当![]() 时,
时,![]() 故
故![]() 时,
时,![]() 函数
函数![]() 单调递减,
单调递减,![]() 时,
时,![]() 函数
函数![]() 单调递增;
单调递增;
(2)当![]() 时,故
时,故![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
(3)当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 单调递增;
单调递增;
(4)当![]() 时,故
时,故![]() 时,
时,![]() 函数
函数![]() 单调递增,
单调递增,
![]() 时,
时,![]() 函数
函数![]() 单调递减,
单调递减,
![]() 时,
时,![]() 函数
函数![]() 单调递增;
单调递增;
(Ⅱ)当![]() 时,
时,![]() 有唯一零点
有唯一零点![]() 不符合题意;
不符合题意;
由(Ⅰ)知:当![]() 时,故
时,故![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() 时,函数
时,函数![]() 单调递增,
单调递增,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,![]() 必有两个零点;
必有两个零点;
当![]() 时,故
时,故![]() 时,函数
时,函数![]() 单调递增,
单调递增,
![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() 时,函数
时,函数![]() 单调递增,
单调递增,![]() ,函数
,函数![]() 至多有一个零点;
至多有一个零点;
当![]() 时,函数
时,函数![]() 单调递增,函数
单调递增,函数![]() 至多有一个零点;
至多有一个零点;
当![]() 时,故
时,故![]() 时,函数
时,函数![]() 单调递增,
单调递增,![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() 时,函数
时,函数![]() 单调递增,
单调递增,![]() ,函数
,函数![]() 至多有一个零点;
至多有一个零点;
综上所述:当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江苏省淮阴中学科技兴趣小组在计算机上模拟航天器变轨返回试验.设计方案如图,航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() .观测点
.观测点![]() 同时跟踪航天器,试问:当航天器在
同时跟踪航天器,试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() ,
,![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为![]()
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴正方向向右平移
轴正方向向右平移![]() 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,当
的图象,当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.
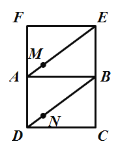
(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +xlnx,g(x)=x3﹣x2﹣3.
+xlnx,g(x)=x3﹣x2﹣3.
(1)讨论函数h(x)=![]() 的单调性;
的单调性;
(2)如果对任意的s,t∈[![]() ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .记“
.记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com