
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,对任意的
,对任意的![]()
![]() 且
且![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)解不等式![]() ;
;
(3)若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用函数单调性的定义,结合函数![]() 为奇函数以及题目所给已知条件,证得
为奇函数以及题目所给已知条件,证得![]() ,由此判断出函数
,由此判断出函数![]() 在
在![]() 上递增.(2)根据函数的定义域和单调性列不等式组,解不等式组求得不等式的解集.(3)根据
上递增.(2)根据函数的定义域和单调性列不等式组,解不等式组求得不等式的解集.(3)根据![]() 的单调性,将问题转化为
的单调性,将问题转化为![]() ,对
,对![]() 恒成立问题来求解,构造函数
恒成立问题来求解,构造函数![]() ,结合一次函数的性质列不等式,解不等式求得
,结合一次函数的性质列不等式,解不等式求得![]() 的取值范围.
的取值范围.
(1)证明任取![]() 且
且![]() ,则
,则![]() ,
,
∵![]() 为奇函数,∴
为奇函数,∴![]() ,
,
∴![]()
由已知得![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
(2)∵![]() 在
在![]() 上单调递增,∴
上单调递增,∴ ,解得
,解得![]() .
.
![]() 不等式的解集为
不等式的解集为![]()
(3)∵![]() ,
,![]() 在
在![]() 上单调递增,∴在
上单调递增,∴在![]() 上,
上,![]() .
.
问题转化为![]() ,即
,即![]() ,对
,对![]() 恒成立.
恒成立.
设![]() .
.
①若![]() ,则
,则![]() ,对
,对![]() 恒成立.
恒成立.
②若![]() ,则
,则![]() 为
为![]() 的一次函数,若
的一次函数,若![]() ,对
,对![]() 恒成立,必须
恒成立,必须![]() ,且
,且![]() ,∴
,∴![]() 或
或![]() .
.
∴![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),设函数f(x)=
cosωx),设函数f(x)= ![]()
![]() +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ![]() ,1)
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ![]() ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某班35名学生的投篮成绩(每人投一次)的条形统计图,其中上面部分数据破损导致数据不完全。已知该班学生投篮成绩的中位数是5,则根据统计图,则下列说法错误的是( )

A. 3球以下(含3球)的人数为10
B. 4球以下(含4球)的人数为17
C. 5球以下(含5球)的人数无法确定
D. 5球的人数和6球的人数一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.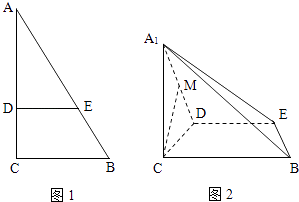
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com