【题目】己知正实数
、
满足
，则
的最小值是______.
【答案】10
【解析】
由
得，
，设直线l的方程为
，则
，
，
都在直线l上，作出
的与斜边AB相切的旁切圆，设圆心
，由旁切圆的性质可知，圆P的周长
，根据几何关系可得，
，由此即可求得结果.
由得，，设直线l的方程为，且
，
，
则，，都在直线l上，如图，
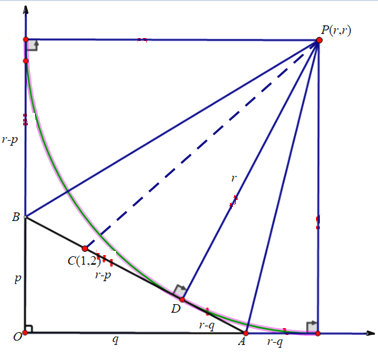
圆P是的与斜边AB相切的旁切圆，设圆心，由旁切圆的性质可知，
的周长，根据几何关系可得，，
即
，化简可得，
，解得
或
（舍去），
所以
，即
的最小值为10.
故答案为：10.
【点晴】
本题考查平面几何的几何关系，直角三角形旁切圆的性质，以及直线方程的应用，着重考查转化与化归的能力和数形结合的思想运用，设出直线AB的截距式方程和作出旁切圆的图象是解决本题的关键，属难题.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】设函数
的定义城为D，若满足条件：存在
，使在
上的值城为
（
且
），则称为“k倍函数”，给出下列结论：①
是“1倍函数”；②
是“2倍函数”：③
是“3倍函数”．其中正确的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
是椭圆
上的点，
，
是焦点，离心率
.
（1）求椭圆的方程；
（2）设
，
是椭圆上的两点，且
，（
是定数），问线段
的垂直平分线是否过定点？若过定点，求出此定点的坐标，若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：吨）和年利润
（单位：万元）的影响．对近六年的年宣传费
和年销售量
（
）的数据作了初步统计，得到如下数据：
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式
（
）．对上述数据作了初步处理，得到相关的值如表：
|
|
|
|
|
|
|
|
（1）根据所给数据，求关于的回归方程；
（2）已知这种产品的年利润与，的关系为
若想在
年达到年利润最大，请预测年的宣传费用是多少万元？
附：对于一组数据
，
，…，
，其回归直线
中的斜率和截距的最小二乘估计分别为
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知数列
：1，
，，3，3，3，
，，，，…，
，即当
（
）时，
，记
（
）．
（1）求
的值；
（2）求当
（），试用n、k的代数式表示
（）；
（3）对于
，定义集合
是
的整数倍，，且
，求集合
中元素的个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数
（其中
）.
（1）判断函数
的奇偶性，并说明理由；
（2）求函数的反函数
（3）若两个函数
与
在区间
上恒满足
，则函数与在闭区间上是分离的．试判断的反函数
与
在闭区间
上是否分离？若分离，求出实数
的取值范围；若不分离，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
